7 境界条件を満たす解とその一意性
本節では、いよいよ元の問題の境界条件 (5) を
満たす解を考えることにする。
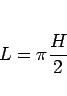 |
(36) |
の場合は、これまでの考察から、
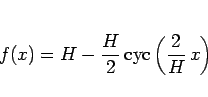 |
(37) |
が丁度境界条件 (5) を満たす解 (のひとつ) となる。
では、(36) ではない場合はどうだろうか。
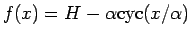 が B を通る条件は、
が B を通る条件は、
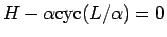 , すなわち
, すなわち
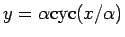 が
点 (
が
点 ( ) を通ることと同じであるが、
もし、
) を通ることと同じであるが、
もし、
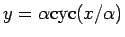 の曲線が、
複数の
の曲線が、
複数の 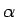 に対して交差することがあれば、
A, B を通る逆さサイクロイドが 2 つ存在してしまう可能性があるが、
に対して交差することがあれば、
A, B を通る逆さサイクロイドが 2 つ存在してしまう可能性があるが、
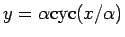 (
(
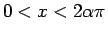 ) のグラフを
複数の
) のグラフを
複数の 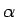 について書いてみると図 6 の
ようになり、交差がないだろうことが予想できる。
について書いてみると図 6 の
ようになり、交差がないだろうことが予想できる。
図 6:
複数の 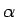 に対するサイクロイド関数のグラフ
に対するサイクロイド関数のグラフ
|
|
これらの関数のグラフに交差がなく、第 1 象限を埋めつくしていることを
以下でちゃんと示してみる。
すなわち、任意の 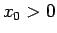 ,
, 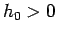 に対して、
に対して、
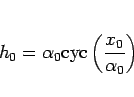 |
(38) |
となる 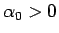 が常に存在し、
かつそのような
が常に存在し、
かつそのような 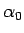 はただ一つしかないことを示す。
はただ一つしかないことを示す。
(38) をパラメータで表せば、
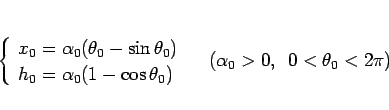 |
(39) |
となるので、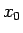 ,
, 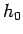 に対し、
このような
に対し、
このような 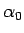 ,
, 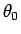 がただ一組存在することを示せばよい。
(39) より、
がただ一組存在することを示せばよい。
(39) より、
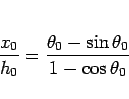 |
(40) |
となるが、まずこれを満たす 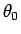 が一意に存在することを示す。
そのために、今
が一意に存在することを示す。
そのために、今
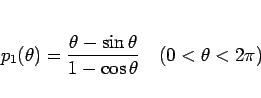
という関数を考える。
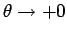 では、
では、
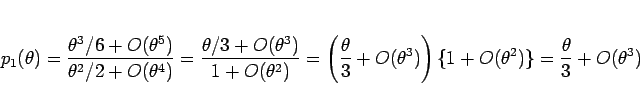
なので 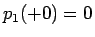 で、また
で、また
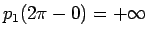 も容易にわかるので、
あとは
も容易にわかるので、
あとは
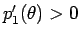 (
(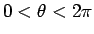 ) を示せば、
) を示せば、
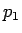 が
が 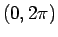 から
から 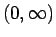 の 1 対 1 の関数であることになり、
よって (40) を満たす
の 1 対 1 の関数であることになり、
よって (40) を満たす 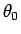 がただ一つ、
常に存在することがわかる。
がただ一つ、
常に存在することがわかる。
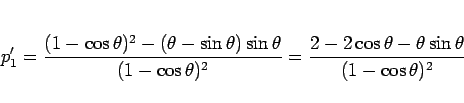
となるが、この分子を
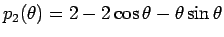 とすると、
とすると、
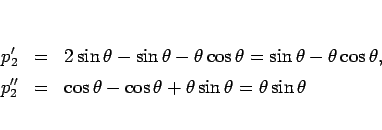
より、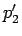 の増減表は以下のようになる。
よって、
の増減表は以下のようになる。
よって、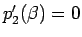 ,
,
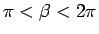 となる
となる 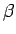 があり、
それを境に
があり、
それを境に 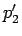 の符号が変わるので、
の符号が変わるので、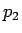 の増減表は以下のようになる。
よって
の増減表は以下のようになる。
よって 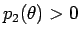 (
(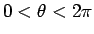 ) となることがわかり、
) となることがわかり、
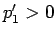 、すなわち
、すなわち 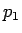 が
が 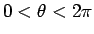 で単調なことが示され、
(40) となる
で単調なことが示され、
(40) となる 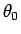 の一意存在が示された。
の一意存在が示された。
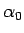 の方は、(39) により
の方は、(39) により
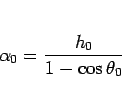
と一意に決定する。よって、これにより (39) を
満たす 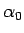 ,
, 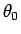 が、ただ一組、
そして常に存在することが示された。
が、ただ一組、
そして常に存在することが示された。
結局、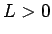 ,
, 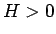 の場合、すべての A, B に対して、
それを通る逆さサイクロイド (
の場合、すべての A, B に対して、
それを通る逆さサイクロイド (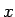 ,
, 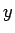 方向に同じ比率で拡大したもの) が、
ただ一つ存在することになる。
方向に同じ比率で拡大したもの) が、
ただ一つ存在することになる。
なお、与えられた 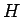 ,
, 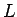 からそのようなサイクロイドを書くための
車輪の半径
からそのようなサイクロイドを書くための
車輪の半径 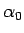 を知ることは、あまり容易ではなく、
を知ることは、あまり容易ではなく、
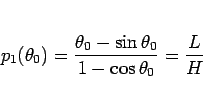
となる 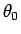 をまず取らなければいけないが、
これは超越方程式であり、コンピュータによる数値計算は可能だろうが、
式の上で値を求めるのは容易ではない。
しかし、図の上でそれを行うには、例えば次のようにすればよい。
をまず取らなければいけないが、
これは超越方程式であり、コンピュータによる数値計算は可能だろうが、
式の上で値を求めるのは容易ではない。
しかし、図の上でそれを行うには、例えば次のようにすればよい。
- 高さ
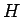 , 横
, 横 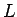 の長方形 ACBD の左下 C から右上 D への対角線を引く。
の長方形 ACBD の左下 C から右上 D への対角線を引く。
- 左下角から適当に小さい半径 (
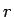 ) の輪を使ってサイクロイドを書き、
そのサイクロイドと対角線との交点 P を取る。
輪の 1 点に目印をつけておいて、長方形の底辺に沿って輪を
すべらないようにころがせば、実際にはサイクロイドの線を書かなくても
P を見つけることは可能だと思われる。
) の輪を使ってサイクロイドを書き、
そのサイクロイドと対角線との交点 P を取る。
輪の 1 点に目印をつけておいて、長方形の底辺に沿って輪を
すべらないようにころがせば、実際にはサイクロイドの線を書かなくても
P を見つけることは可能だと思われる。
- P の真下の高さ
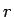 の点 Q を取り、
CQ を延長して長方形の右の辺との交点 R を取れば、
その R の高さが求める
の点 Q を取り、
CQ を延長して長方形の右の辺との交点 R を取れば、
その R の高さが求める 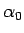 となる (図 7)。
となる (図 7)。
図 7:
サイクロイドの半径 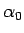 の作図
の作図
|
|
これで 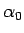 が求まることは、以下のようにしてわかる。
まず、P(
が求まることは、以下のようにしてわかる。
まず、P(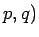 とすると、
とすると、
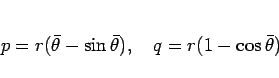
となる 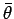 が存在するが、
が存在するが、
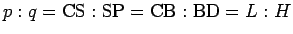 なので、
なので、
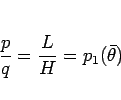
となり、よって
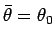 となることがわかる。
となることがわかる。
また、
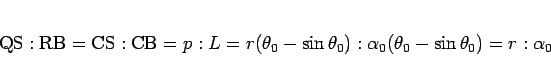
なので、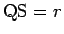 より
より
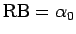 となることがわかる。
となることがわかる。
サイクロイドを書く手順がやや面倒だろうが、
このようにして半径 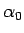 がある程度作図できれば、
逆さサイクロイドもある程度手動で作図できるかもしれない。
がある程度作図できれば、
逆さサイクロイドもある程度手動で作図できるかもしれない。
竹野茂治@新潟工科大学
2016年1月8日
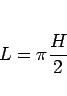
![]() が B を通る条件は、
が B を通る条件は、
![]() , すなわち
, すなわち
![]() が
点 (
が
点 (![]() ) を通ることと同じであるが、
もし、
) を通ることと同じであるが、
もし、
![]() の曲線が、
複数の
の曲線が、
複数の ![]() に対して交差することがあれば、
A, B を通る逆さサイクロイドが 2 つ存在してしまう可能性があるが、
に対して交差することがあれば、
A, B を通る逆さサイクロイドが 2 つ存在してしまう可能性があるが、
![]() (
(
![]() ) のグラフを
複数の
) のグラフを
複数の ![]() について書いてみると図 6 の
ようになり、交差がないだろうことが予想できる。
について書いてみると図 6 の
ようになり、交差がないだろうことが予想できる。
![]() ,
, ![]() に対して、
に対して、
![]() の方は、(39) により
の方は、(39) により
![]() ,
, ![]() の場合、すべての A, B に対して、
それを通る逆さサイクロイド (
の場合、すべての A, B に対して、
それを通る逆さサイクロイド (![]() ,
, ![]() 方向に同じ比率で拡大したもの) が、
ただ一つ存在することになる。
方向に同じ比率で拡大したもの) が、
ただ一つ存在することになる。
![]() ,
, ![]() からそのようなサイクロイドを書くための
車輪の半径
からそのようなサイクロイドを書くための
車輪の半径 ![]() を知ることは、あまり容易ではなく、
を知ることは、あまり容易ではなく、
![]() が求まることは、以下のようにしてわかる。
まず、P(
が求まることは、以下のようにしてわかる。
まず、P(![]() とすると、
とすると、
![]() がある程度作図できれば、
逆さサイクロイドもある程度手動で作図できるかもしれない。
がある程度作図できれば、
逆さサイクロイドもある程度手動で作図できるかもしれない。