12 ころがる場合
次は、すべらずにころがる場合を考える。
この場合も細かく考えると色々問題がある。
- 問題 1.
ころがる場合は、基本的には「摩擦力」が働いているが、
それは 10 節で考察した「動摩擦力」ではなく、
物体と斜面の接点がすべらない「静止摩擦力」が働く。
そして、すべらないためには、
その摩擦力が最大摩擦力である 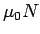 を越えてはいけないので、
ある程度垂直抗力が大きくなければいけない。
よって、初速度 0 ですべる場合の最速解のように
出発点の傾きが
を越えてはいけないので、
ある程度垂直抗力が大きくなければいけない。
よって、初速度 0 ですべる場合の最速解のように
出発点の傾きが  となることは許されず、
静止摩擦係数
となることは許されず、
静止摩擦係数 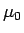 による制限 (下限) がつく。
による制限 (下限) がつく。
 の場所では、斜面の傾きの変化による遠心力の反作用も
垂直抗力に加わるので、すべらないための条件はさらにややこしくなる。
の場所では、斜面の傾きの変化による遠心力の反作用も
垂直抗力に加わるので、すべらないための条件はさらにややこしくなる。
- 問題 2.
ころがる場合は、モーメントのつりあいも考える必要があるが、
ころがる物体 (通常は円柱や球) の慣性モーメント 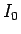 は、
円柱 (
は、
円柱 (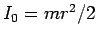 ) にしても球 (
) にしても球 (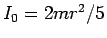 ) にしても、
小さいながらも半径
) にしても、
小さいながらも半径 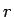 を持つ物体であり、
運動方程式はその物体の重心、すなわち斜面
を持つ物体であり、
運動方程式はその物体の重心、すなわち斜面 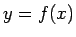 から
距離
から
距離 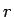 だけ離れた点に対して考える必要があり、
そのため重心の移動は
だけ離れた点に対して考える必要があり、
そのため重心の移動は 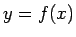 とは少し異なる軌跡となる。
このような曲線の等距離曲線は、一般にはかなり厄介で、
元の曲線が簡単な式であっても等距離曲線は
かなり難しい式になることが多い。
とは少し異なる軌跡となる。
このような曲線の等距離曲線は、一般にはかなり厄介で、
元の曲線が簡単な式であっても等距離曲線は
かなり難しい式になることが多い。
- 問題 3.
物体の半径 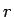 を無視せずに正の値と考える場合、
斜面の曲率
を無視せずに正の値と考える場合、
斜面の曲率 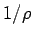 にも制限がつく。
物体が常に 1 点で接する状態でないと、
滑らかな運動にはならないし、運動が止まる可能性もあるので、
曲率半径
にも制限がつく。
物体が常に 1 点で接する状態でないと、
滑らかな運動にはならないし、運動が止まる可能性もあるので、
曲率半径 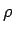 は
は 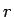 より大きくなければならない。
より大きくなければならない。
以上の問題点を考慮に入れ、改めて運動方程式から検討し直す。
物体と斜面との接点は今まで通り 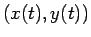 (点
(点 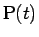 ) とし、
物体の重心を
) とし、
物体の重心を 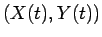 (点
(点 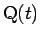 ) と書くことにする (図 12)。
) と書くことにする (図 12)。
物体の回転半径を 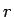 、慣性モーメントを
、慣性モーメントを 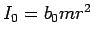 とする。
とする。
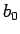 は円柱ならば
は円柱ならば 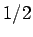 、球ならば
、球ならば 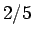 なので
なので 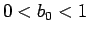 の定数としておく。
の定数としておく。
初速度は 0 とし、境界条件は、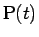 に対して成り立つとしておく。
に対して成り立つとしておく。
 |
(85) |
まず、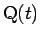 は
は 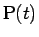 から見て斜面の垂直方向にあるので、
その関係は
から見て斜面の垂直方向にあるので、
その関係は
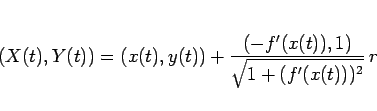 |
(86) |
となる。運動方程式は、重心に対して立てると、
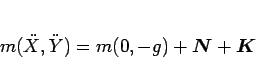 |
(87) |
であり、
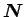 は垂直抗力、
は垂直抗力、
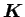 は
は 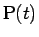 に働く静止摩擦力で、
に働く静止摩擦力で、
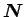 は斜面の垂直方向、
は斜面の垂直方向、
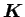 は接線方向なので、
は接線方向なので、
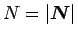 ,
,
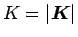 とすれば
とすれば
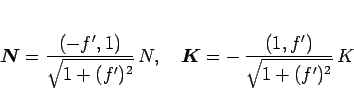 |
(88) |
となり、問題 1 で述べたように静止摩擦力は、最大静止摩擦力 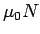 よりも
小さくなくてはならない。
よりも
小さくなくてはならない。
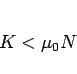 |
(89) |
一方、回転に対する運動方程式は、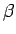 を回転の角加速度とすれば
を回転の角加速度とすれば
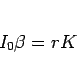 |
(90) |
となる。これを少し細かく見てみる。
出発時からの回転角を 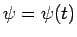 とし (時計回り)、
とし (時計回り)、
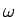 をその角速度とすると、
をその角速度とすると、
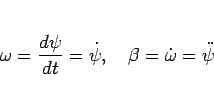
となる。直線斜面ではないのでこの  もやや複雑であるが、
それを求めるため、各
もやや複雑であるが、
それを求めるため、各  での斜面の仰角を
での斜面の仰角を 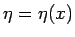 (反時計回り) とする (
(反時計回り) とする (
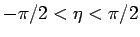 )。
)。
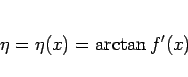 |
(91) |
少なくとも 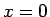 では
では 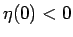 となる。
となる。
出発点で
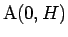 と接していた円周上の点を
と接していた円周上の点を 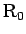 、
、
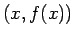 での円周上の接点を
での円周上の接点を 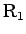 と
すると (図 13)、
と
すると (図 13)、
A から 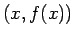 までの曲線路の長さ
までの曲線路の長さ 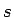 は
は
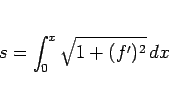
であり、これは円周上の
 の弧長に等しい。
回転角
の弧長に等しい。
回転角 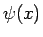 は、その弧の中心角から、
斜面の垂直方向の角度の差
は、その弧の中心角から、
斜面の垂直方向の角度の差
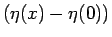 を引いたものになるので、
を引いたものになるので、
となる。よって、角速度 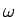 は
は
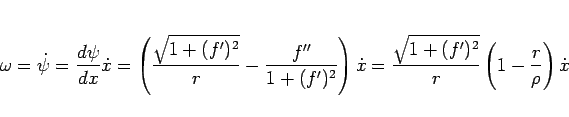 |
(93) |
となる。ここで、
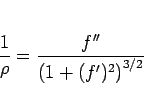 |
(94) |
は曲線 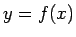 の曲率、
の曲率、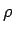 は曲率半径である。
本節冒頭の問題 3 より
は曲率半径である。
本節冒頭の問題 3 より 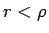 でないと
いけないから (93) の係数
でないと
いけないから (93) の係数 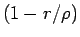 は正となる。
は正となる。
次に、今までと同様に、(87) から 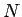 を消去して
エネルギー保存の式を導くことを考える。
(87) を成分でみると、
を消去して
エネルギー保存の式を導くことを考える。
(87) を成分でみると、
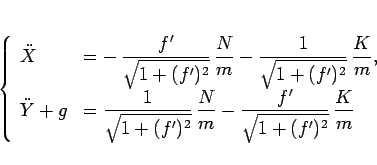
なので、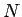 ,
, 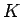 を消去すると、それぞれ次の式が得られる。
を消去すると、それぞれ次の式が得られる。
この (95) をエネルギー保存則の形に変形する
ことを考えるが、そのためにまず
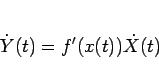 |
(97) |
が成り立つことを示す。
(91) より
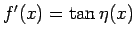 なので、
なので、
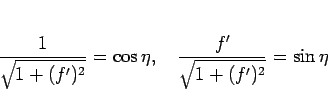
と書け、よって (86) より
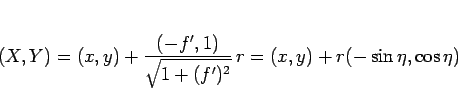
となるから、
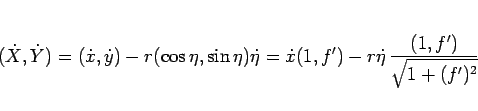 |
(98) |
となり、これは 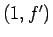 に平行なので、
確かに (97) が成り立つことがわかる。
に平行なので、
確かに (97) が成り立つことがわかる。
なお、
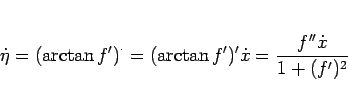
なので、(98) の
重心の移動速度
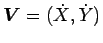 は、
は、
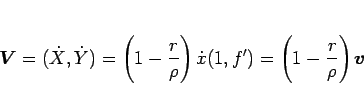 |
(99) |
となる。これと (93)、および 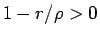 より、
より、
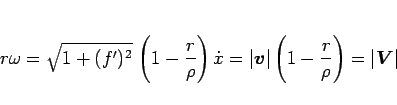 |
(100) |
もわかる。
さて、(95) に戻るが、
この式を 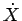 倍すると、(97) より、
倍すると、(97) より、
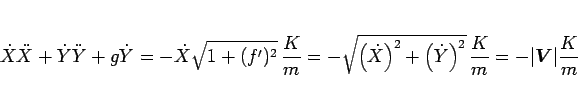 |
(101) |
となるが、この右辺と回転エネルギー 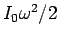 との関係を見てみる。
このエネルギーを
との関係を見てみる。
このエネルギーを 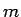 で割ったものを
で割ったものを 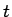 で微分すると、
で微分すると、
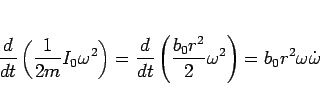
であり、(90) より
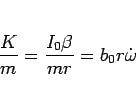
なので、(100) より
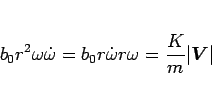
となる。
よって、結局 (101) は、
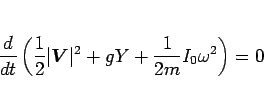 |
(102) |
と変形できることがわかる。
これは運動エネルギーと位置エネルギーと回転エネルギー
の総和が保存されることを意味する (物理学なら、むしろここからスタートするだろう)。
これを積分すれば、
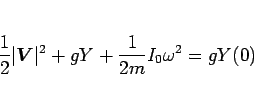 |
(103) |
となる。ここで、
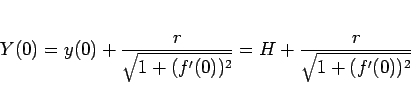 |
(104) |
である。
(100) より、
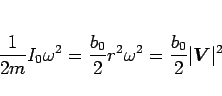
なので、(103) は、
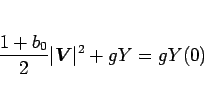
となり、これは
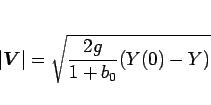 |
(105) |
と変形できるが、(99) より
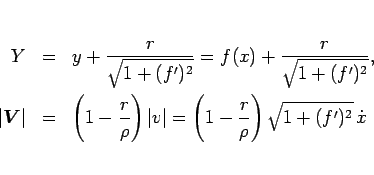
なので、
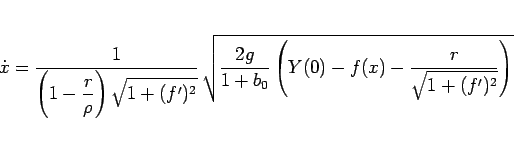
と書ける。よって、A から B までころがり落ちる時間 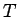 は
は
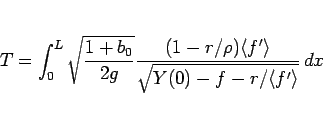 |
(106) |
と表わされることになる。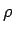 は (94) の式で
は (94) の式で
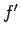 と
と 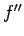 で与えられるため、
この右辺の被積分関数は
で与えられるため、
この右辺の被積分関数は 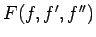 の形をしていることがわかる。
よって、この積分の最小値を与える関数
の形をしていることがわかる。
よって、この積分の最小値を与える関数 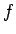 がころがる場合の
最速降下線となる。
がころがる場合の
最速降下線となる。
なお、ここまでは 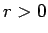 であるとして、重心が曲線上にないとして
方程式を考えてきたが、通常のように
であるとして、重心が曲線上にないとして
方程式を考えてきたが、通常のように 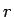 が十分小さいとして無視する、
すなわち
が十分小さいとして無視する、
すなわち
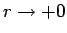 としてみると、(106) は
としてみると、(106) は
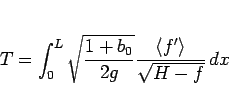 |
(107) |
となり、これはすべる場合の時間 (11) と 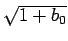 倍
の違いしかないことがわかる。
よって、その場合の最速解はやはり逆さサイクロイドとなる。
しかし、それは出発点の傾きが
倍
の違いしかないことがわかる。
よって、その場合の最速解はやはり逆さサイクロイドとなる。
しかし、それは出発点の傾きが 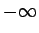 になってしまい、
本節の最初に述べた問題 1 の条件を考えれば
その逆さサイクロイドの解は適切ではない。
になってしまい、
本節の最初に述べた問題 1 の条件を考えれば
その逆さサイクロイドの解は適切ではない。
この、 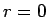 と見た場合に、
(89) の条件を満たす最速解があるかどうかは
よくわからない。
と見た場合に、
(89) の条件を満たす最速解があるかどうかは
よくわからない。
さて、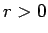 の場合に戻って、(106) の変分を考える。
の場合に戻って、(106) の変分を考える。
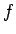 が右辺の積分の最小値を与える解であるとき、
が右辺の積分の最小値を与える解であるとき、
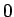 ,
, 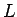 の付近で 0 となる
の付近で 0 となる 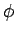 に対して、
に対して、
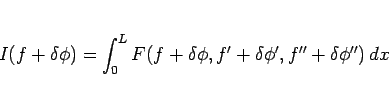
は、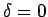 で極小となるから、
で極小となるから、
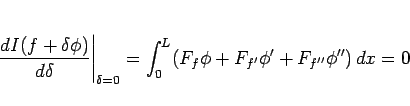
となる。よって部分積分をすれば、
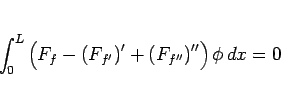
となるので、この場合のオイラー方程式は、
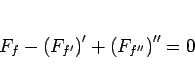 |
(108) |
となることがわかる。
やや複雑だが、(106) に対してこの式を計算してみる。
なお、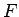 に定数倍として含まれている
に定数倍として含まれている
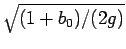 の部分は
もちろん無視してよい。
(94) より
の部分は
もちろん無視してよい。
(94) より 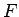 は
は 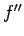 に
関して 1 次式なので
に
関して 1 次式なので
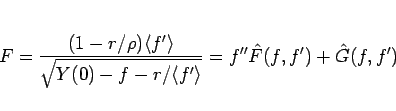
として計算を行う。ここで、
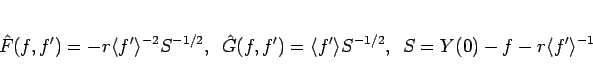 |
(109) |
である。
(108) の左辺は 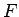 に関して線形だから、
に関して線形だから、
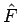 に関する式 (=
に関する式 (= 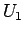 とする) と
とする) と 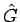 に関する式 (=
に関する式 (= 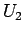 とする) の和に分けることができ、
まずそのそれぞれを計算してみる。
とする) の和に分けることができ、
まずそのそれぞれを計算してみる。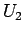 は
は
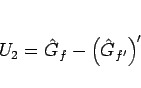
となるが、これは 4 節の (18) を
導くところで見たように、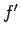 倍すれば
倍すれば
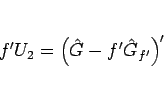
と変形できる。一方 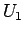 は、
は、
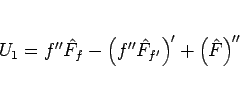 |
(110) |
となるが、
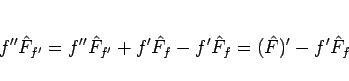
と変形すれば、
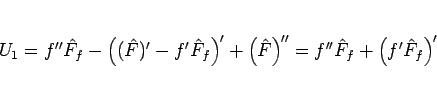
となるから、これを 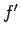 倍すれば
倍すれば
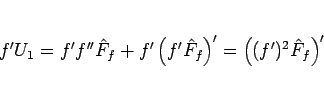 |
(111) |
となることがわかる。
結局、(108) を 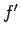 倍したものは、
倍したものは、
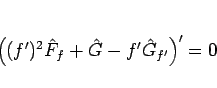
と書けることになり、よって
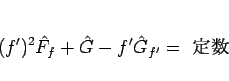 |
(112) |
と積分できる。今の場合、
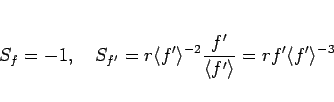
なので、
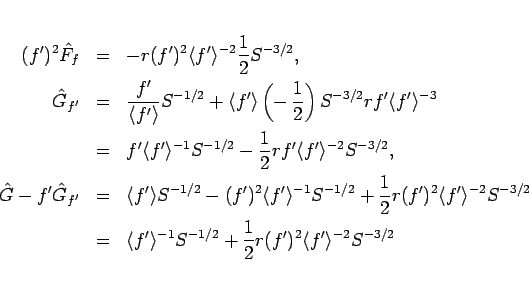
となり、結局 (112) は、
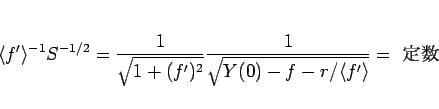 |
(113) |
だけが残る。
ここで、
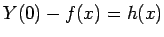 とすれば、
とすれば、
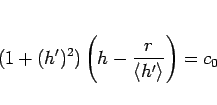 |
(114) |
と、(20) に対応した 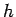 の 1 階変数分離形の方程式が得られることになる。
しかし、これを積分して
の 1 階変数分離形の方程式が得られることになる。
しかし、これを積分して 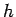 を
を 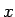 の式で表すのは容易ではない。
の式で表すのは容易ではない。
(114) を展開すれば、
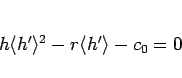
となるが、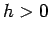 ,
, 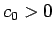 ,
, 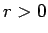 ,
,
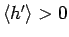 より、
より、
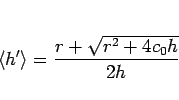
となり、
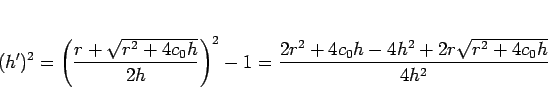
となるので、
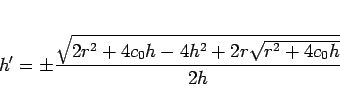
が得られる。しかし、見てわかるように、
この方程式の求積は容易ではない。
なお、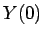 は (104) で与えられるので、
は (104) で与えられるので、
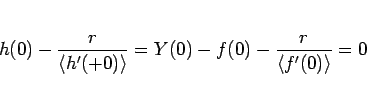
となるから、(114) を展開した
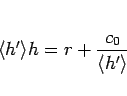
で
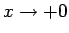 とすると
とすると
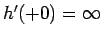 でなければいけないことがわかる。
つまり、この (114) の解による
でなければいけないことがわかる。
つまり、この (114) の解による 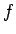 は
は
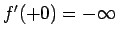 と
なり、やはり問題 1 の条件は満たさない。
と
なり、やはり問題 1 の条件は満たさない。
すなわち、ころがりの問題を考えると、変分法で得られる関数は
問題 1 の条件に適する解にはならないので、
問題 1 を満たしながら (106) を最小にする解は
存在しない可能性もあるが、よくはわからない。
問題 1 の条件を満たすような解を存在させるためには、
例えば 11 節のように、
正の初速度を与える必要があるかもしれない。
また上では、斜面上の接点 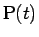
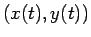 の軌跡に
関する方程式を考えたが、
その解に対する重心
の軌跡に
関する方程式を考えたが、
その解に対する重心 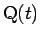
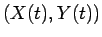 の軌跡をついでに
考えてみよう。
の軌跡をついでに
考えてみよう。
その軌跡が
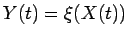 で表されるとすると、
これを
で表されるとすると、
これを 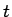 で微分すれば、
で微分すれば、
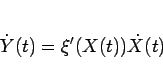
となるが、(97) より、
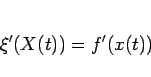 |
(115) |
であることがわかる。また、(86) より
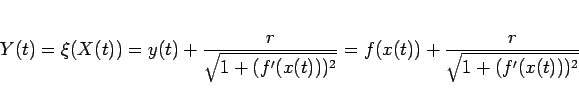
なので、これらを (113) に代入すると
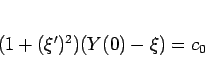 |
(116) |
となるので、よって
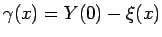 とすれば
とすれば 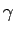 は (20) と同じ方程式を満たし、
は (20) と同じ方程式を満たし、
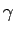 はサイクロイド (の
はサイクロイド (の 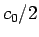 倍) を
平行移動したものになることがわかる。
倍) を
平行移動したものになることがわかる。
すなわち、ころがる場合のオイラー方程式の解は、
重心が逆さサイクロイドを平行移動した軌道を取り、
斜面はそこから距離 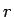 だけ下に離れた等距離曲線となる。
もちろん、問題 1 の条件を満たさない問題があるので、
これにより最速解が決定したとは言いづらいが、
問題 1、すなわち条件 (89) を
無視すればこれが解となる。
だけ下に離れた等距離曲線となる。
もちろん、問題 1 の条件を満たさない問題があるので、
これにより最速解が決定したとは言いづらいが、
問題 1、すなわち条件 (89) を
無視すればこれが解となる。
実は、重心の軌道がサイクロイドとなることは、
式 (105) からも示唆される。
なお、この等距離曲線、
すなわちサイクロイド
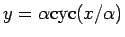 から
から 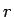 だけ
上に離れた曲線を表す式 (
だけ
上に離れた曲線を表す式 (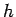 の方) を
以下で求めてみる (図 14)。
の方) を
以下で求めてみる (図 14)。
このサイクロイド
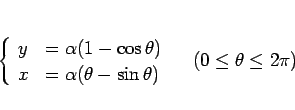
の、パラメータ 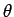 に対応する点での傾きは
に対応する点での傾きは
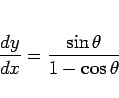
なので、その法線方向は
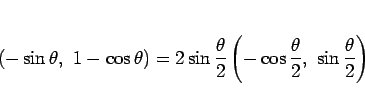
となる。よって、サイクロイドから 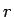 だけ上に離れた関数は、
だけ上に離れた関数は、
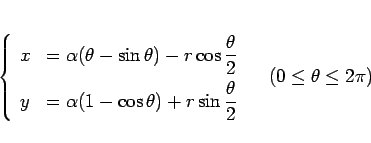 |
(117) |
とパラメータ表示されることがわかる。
これを  と書くことにする。
と書くことにする。
この 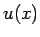 が、実際に
が、実際に 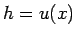 として方程式 (114) を
満たすことを示そう。
として方程式 (114) を
満たすことを示そう。
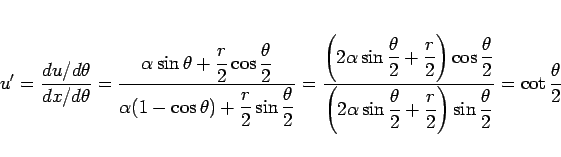
より、
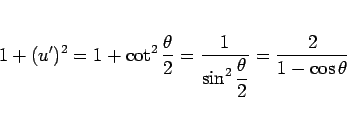
となるので、
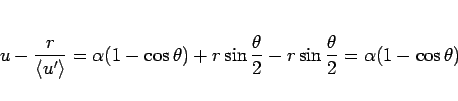
となり、よって
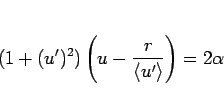
となるので、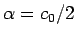 の
の 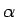 に対して
に対して 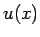 は (114) を満たす解となる。
あとは境界条件を満たすよう適宜平行移動すれば、
問題 1 の条件を無視したものではあるが、
(106) を最小化する解が得られることになる。
は (114) を満たす解となる。
あとは境界条件を満たすよう適宜平行移動すれば、
問題 1 の条件を無視したものではあるが、
(106) を最小化する解が得られることになる。
竹野茂治@新潟工科大学
2016年1月8日
![]() (点
(点 ![]() ) とし、
物体の重心を
) とし、
物体の重心を ![]() (点
(点 ![]() ) と書くことにする (図 12)。
) と書くことにする (図 12)。
![]() に対して成り立つとしておく。
に対して成り立つとしておく。
![]() と接していた円周上の点を
と接していた円周上の点を ![]() 、
、
![]() での円周上の接点を
での円周上の接点を ![]() と
すると (図 13)、
と
すると (図 13)、
![]() を消去して
エネルギー保存の式を導くことを考える。
(87) を成分でみると、
を消去して
エネルギー保存の式を導くことを考える。
(87) を成分でみると、
![]() 倍すると、(97) より、
倍すると、(97) より、
![]() であるとして、重心が曲線上にないとして
方程式を考えてきたが、通常のように
であるとして、重心が曲線上にないとして
方程式を考えてきたが、通常のように ![]() が十分小さいとして無視する、
すなわち
が十分小さいとして無視する、
すなわち
![]() としてみると、(106) は
としてみると、(106) は
![]() と見た場合に、
(89) の条件を満たす最速解があるかどうかは
よくわからない。
と見た場合に、
(89) の条件を満たす最速解があるかどうかは
よくわからない。
![]() の場合に戻って、(106) の変分を考える。
の場合に戻って、(106) の変分を考える。
![]() が右辺の積分の最小値を与える解であるとき、
が右辺の積分の最小値を与える解であるとき、
![]() ,
, ![]() の付近で 0 となる
の付近で 0 となる ![]() に対して、
に対して、
![]() に関して線形だから、
に関して線形だから、
![]() に関する式 (=
に関する式 (= ![]() とする) と
とする) と ![]() に関する式 (=
に関する式 (= ![]() とする) の和に分けることができ、
まずそのそれぞれを計算してみる。
とする) の和に分けることができ、
まずそのそれぞれを計算してみる。![]() は
は
![]() は (104) で与えられるので、
は (104) で与えられるので、
![]()
![]() の軌跡に
関する方程式を考えたが、
その解に対する重心
の軌跡に
関する方程式を考えたが、
その解に対する重心 ![]()
![]() の軌跡をついでに
考えてみよう。
の軌跡をついでに
考えてみよう。
![]() で表されるとすると、
これを
で表されるとすると、
これを ![]() で微分すれば、
で微分すれば、
![]() だけ下に離れた等距離曲線となる。
もちろん、問題 1 の条件を満たさない問題があるので、
これにより最速解が決定したとは言いづらいが、
問題 1、すなわち条件 (89) を
無視すればこれが解となる。
だけ下に離れた等距離曲線となる。
もちろん、問題 1 の条件を満たさない問題があるので、
これにより最速解が決定したとは言いづらいが、
問題 1、すなわち条件 (89) を
無視すればこれが解となる。
![]() から
から ![]() だけ
上に離れた曲線を表す式 (
だけ
上に離れた曲線を表す式 (![]() の方) を
以下で求めてみる (図 14)。
の方) を
以下で求めてみる (図 14)。
![]() が、実際に
が、実際に ![]() として方程式 (114) を
満たすことを示そう。
として方程式 (114) を
満たすことを示そう。