11 初速度が正の場合
次は、初速度が 0 ではない場合を考える。
少し勢いをつけて斜面に投げるようなイメージである。
この場合は、元の式 (1)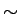 (5) の
うち、(4) が、
(5) の
うち、(4) が、
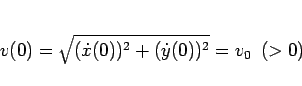 |
(71) |
に変わるが、それにより (10) が、
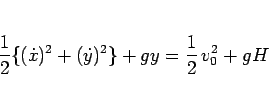 |
(72) |
に変わるので、(11) は
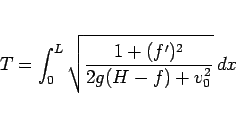 |
(73) |
となる。この場合は、オイラー方程式 (19) は、
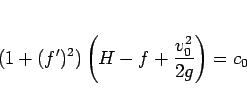 |
(74) |
となるので、
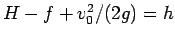 とすれば (20) と
同じ方程式
とすれば (20) と
同じ方程式
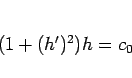
が得られる。この場合、
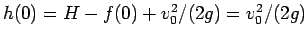 となるので、
(22) は、
となるので、
(22) は、
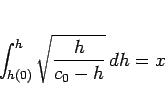
となり、
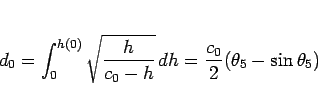 |
(75) |
とすれば
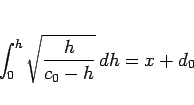
となり、よって、
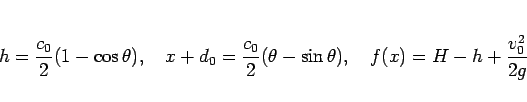 |
(76) |
となる。これは、前の逆さサイクロイドを 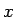 方向に
方向に 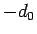 平行移動したものになっている。
平行移動したものになっている。
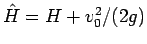 とすると、
とすると、
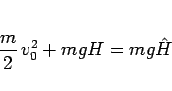
となるので、(76) より、
これは曲線を負の方に少し伸ばして
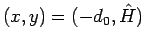 から
速度 0 でスタートして、
から
速度 0 でスタートして、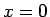 の場所で速さが
の場所で速さが 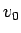 になったものと同じ
状況になっていることがわかる。
また、この解は
になったものと同じ
状況になっていることがわかる。
また、この解は 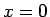 では
では
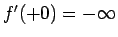 ではなく、
有限な傾きになっている (図 9)。
ではなく、
有限な傾きになっている (図 9)。
図 9:
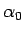 ,
, 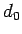 の条件
の条件
|
|
次に、この解が一つに決まるかを考えてみよう。
すなわち、与えられた 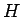 ,
, 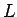 ,
, 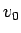 に対して、
に対して、
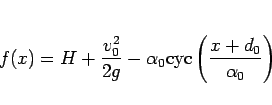 |
(77) |
となる 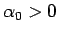 ,
, 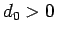 が一意に存在するか
どうかを調べてみる。実際には、
(77) の
が一意に存在するか
どうかを調べてみる。実際には、
(77) の 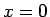 と
と 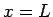 で境界条件 (5) を満たすことが
で境界条件 (5) を満たすことが 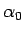 ,
, 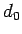 の条件なので、
の条件なので、
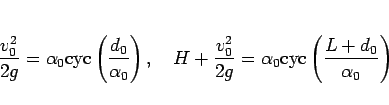 |
(78) |
となる 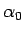 ,
, 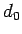 が一意に存在するかどうかを考えればよい (図 10)。
が一意に存在するかどうかを考えればよい (図 10)。
図 10:
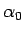 ,
, 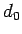 の条件
の条件
|
|
(78) を 2 つのパラメータを用いて
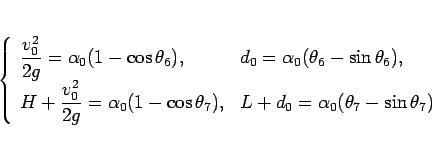 |
(79) |
と表し、それを 4 未知数 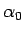 ,
, 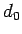 ,
, 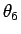 ,
, 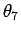 の 4 本の方程式と考え、逆関数定理を用いて解の存在を示す、
という方針もあるが、
ここでは、別の形で (78) の解を
考えていくことにする。
の 4 本の方程式と考え、逆関数定理を用いて解の存在を示す、
という方針もあるが、
ここでは、別の形で (78) の解を
考えていくことにする。
まず、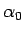 は、サイクロイドが
は、サイクロイドが 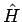 まで達しなければ
いけないので、
まで達しなければ
いけないので、
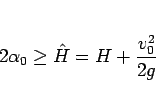 |
(80) |
である必要がある。
このとき、サイクロイド
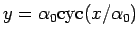 (
(
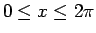 ) と
水平線
) と
水平線 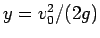 ,
, 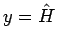 との交点の
との交点の 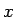 座標を、
小さい方から順に
座標を、
小さい方から順に 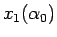 ,
, 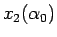 ,
, 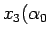 ),
), 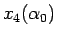 とすると (図 11)、
とすると (図 11)、
図 11:
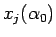
|
|
サイクロイドは 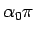 で左右に対称なので、
で左右に対称なので、
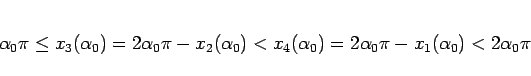
となり、
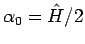 のときは、
そしてそのときだけ
のときは、
そしてそのときだけ
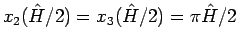 となる。
そして、満たすべき条件 (78) は、
となる。
そして、満たすべき条件 (78) は、
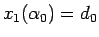 と
と 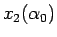 か
か 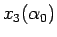 のいずれかが
のいずれかが 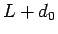 となればよいので、結局任意の
となればよいので、結局任意の 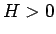 ,
, 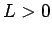 ,
, 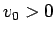 に対して、
に対して、
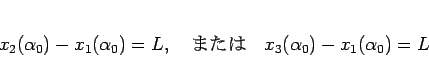 |
(81) |
となるような 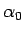 が存在すること、と同じことになる。
そのような
が存在すること、と同じことになる。
そのような 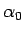 が取れれば、
が取れれば、
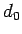 は
は
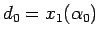 とすればよい。
よって、(81) を満たす
とすればよい。
よって、(81) を満たす 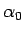 が
ただ一つ存在することを示せばよいが、
それは
が
ただ一つ存在することを示せばよいが、
それは 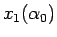 と
と 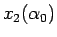 の増減を調べればよく、
一意存在のためには以下のことが言えればよい。
の増減を調べればよく、
一意存在のためには以下のことが言えればよい。
「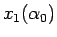 ,
, 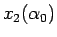 は
は 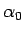 に関して減少関数で、
に関して減少関数で、
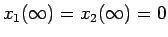 であること、
および
であること、
および
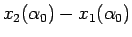 も減少関数であること」
も減少関数であること」
もし、これが示されれば、
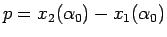 の (80) での値の範囲は
の (80) での値の範囲は
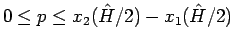 で、
その対応は 1 対 1 となる。
で、
その対応は 1 対 1 となる。
一方
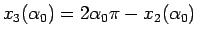 は増加関数で
は増加関数で
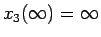 となるので
となるので
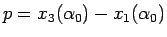 も増加関数で、
(80) での値の範囲は
も増加関数で、
(80) での値の範囲は
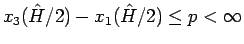 で、
やはり 1 対 1 となる。
で、
やはり 1 対 1 となる。
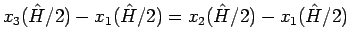 であるから、よってこれにより (81) を
満たす
であるから、よってこれにより (81) を
満たす 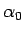 がただ一つ存在することがわかる。
がただ一つ存在することがわかる。
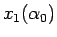 と
と 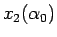 の増減や
の増減や
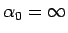 での
値の性質は同じなので、
それについてはとりあえず
での
値の性質は同じなので、
それについてはとりあえず 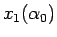 の方のみを考える。
の方のみを考える。
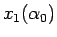 はパラメータを用いて、
はパラメータを用いて、
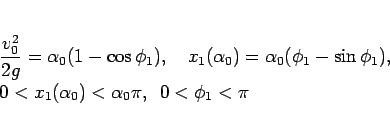 |
(82) |
と表される。ここから、
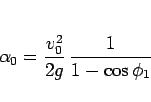
となり、
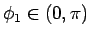 と
と
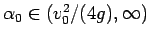 が
1 対 1 に単調 (減少) に対応し、よって
が
1 対 1 に単調 (減少) に対応し、よって 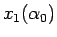 を
パラメータ
を
パラメータ 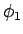 で表現できることになる。
(82) より
で表現できることになる。
(82) より
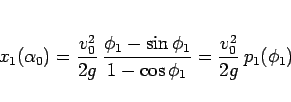
と表されるので、
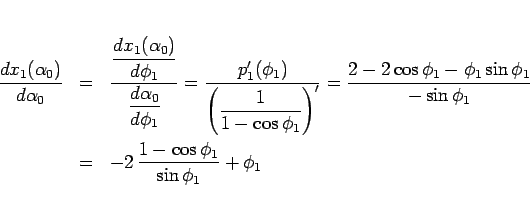
より、
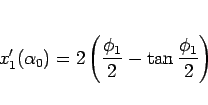 |
(83) |
となる。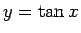 の
の 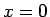 での傾きは 1 なので、
での傾きは 1 なので、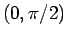 では
では
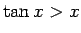 であり、
よって (83) より
であり、
よって (83) より 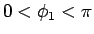 では
では
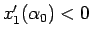 となることがわかる。
よって
となることがわかる。
よって 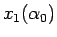 は
は
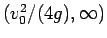 で減少する。
また、両端の値が、
で減少する。
また、両端の値が、
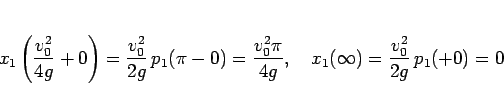
となることもわかる。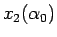 の増減、端点の値も同様なので、
あとは
の増減、端点の値も同様なので、
あとは
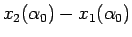 の減少性を示せばよい。
の減少性を示せばよい。
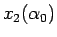 もパラメータを用いて、
もパラメータを用いて、
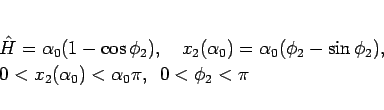 |
(84) |
と表せば、(83) より
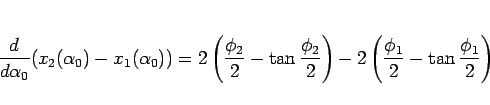
となる (
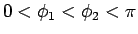 )。ここで、
)。ここで、
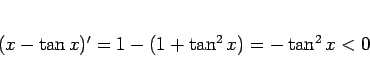
なので、ここから
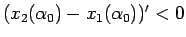 がわかる。
これで
がわかる。
これで
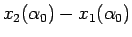 が減少関数であることもわかり、
よって、以上で (81) を
満たす
が減少関数であることもわかり、
よって、以上で (81) を
満たす 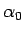 がただひとつ存在することが言え、
初速が正の場合の逆さサイクロイド解が
ただ一つ存在することが示されたことになる。
がただひとつ存在することが言え、
初速が正の場合の逆さサイクロイド解が
ただ一つ存在することが示されたことになる。
竹野茂治@新潟工科大学
2016年1月8日
![]() とすると、
とすると、
![]() ,
, ![]() ,
, ![]() に対して、
に対して、
![]() は、サイクロイドが
は、サイクロイドが ![]() まで達しなければ
いけないので、
まで達しなければ
いけないので、
![]() で左右に対称なので、
で左右に対称なので、
,
は
に関して減少関数で、
であること、 および
も減少関数であること」
![]() は増加関数で
は増加関数で
![]() となるので
となるので
![]() も増加関数で、
(80) での値の範囲は
も増加関数で、
(80) での値の範囲は
![]() で、
やはり 1 対 1 となる。
で、
やはり 1 対 1 となる。
![]() であるから、よってこれにより (81) を
満たす
であるから、よってこれにより (81) を
満たす ![]() がただ一つ存在することがわかる。
がただ一つ存在することがわかる。
![]() と
と ![]() の増減や
の増減や
![]() での
値の性質は同じなので、
それについてはとりあえず
での
値の性質は同じなので、
それについてはとりあえず ![]() の方のみを考える。
の方のみを考える。
![]() はパラメータを用いて、
はパラメータを用いて、
![]() もパラメータを用いて、
もパラメータを用いて、