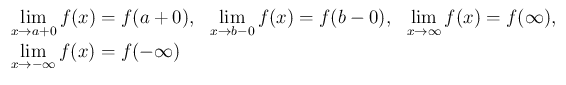 (20)
(20)
それは、片側極限の簡易記法
を利用するもので、以後 (7) を例に説明する。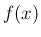 の
の ![$(a,b]$](img34.png) での原始関数を
での原始関数を 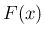 とする。例えば、
とする。例えば、
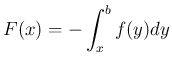
定義による (7) の計算 (21) の場合、 最初に lim の式に書き直すが、 実際にその lim の計算を行うのは原始関数を求めて、 そこに代入を行った後であり、 途中の計算では lim はついてるだけになる。
それに対して、(22) の 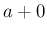 を少し先取りし、
積分範囲の
を少し先取りし、
積分範囲の 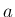 を最初に
を最初に 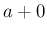 に変えて、
原始関数への代入までは、表面上は lim を書かずに計算するのが
簡易記法の方法である。すなわち、以下のように書く。
に変えて、
原始関数への代入までは、表面上は lim を書かずに計算するのが
簡易記法の方法である。すなわち、以下のように書く。
例えば、(1) の 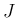 の場合、定義通りに計算すると、
の場合、定義通りに計算すると、
![$\displaystyle J
= \lim_{s\rightarrow +0}\int_s^1 x^{-1/2}dx
= \lim_{s\rightarrow +0}[2x^{1/2}]^1_s
= \lim_{s\rightarrow +0}(2\sqrt{1}-2\sqrt{s})
= 2
$](img94.png)
![$\displaystyle J
= \int_{+0}^1 x^{-1/2}dx
= [2x^{1/2}]^1_{+0}
= 2\sqrt{1}-\lim_{x\rightarrow +0}(2\sqrt{x})
= 2
$](img95.png)
この簡易記法は、他の (6), (8), (9) の
型の広義積分や、合併型の広義積分にも使える。
例えば、
![$\displaystyle \int_{-\infty}^{\infty} \frac{dx}{x^2+1}
= [\arctan x]_{-\infty}^...
...arrow -\infty}\arctan x
= \frac{\pi}{2}\,-\left(-\,\frac{\pi}{2}\right)
= \pi
$](img96.png)
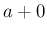 ,
, 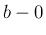 への書き直しも必要ない。
への書き直しも必要ない。
竹野茂治@新潟工科大学