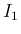
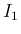 ,
, 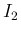 ,
, 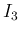 の最終的な形は、
の最終的な形は、
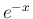 や
や 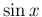 ,
, 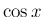 のマクローリン展開の
有限部分を持っている。この節で、その表現を見ておこう。
そのため、関数
のマクローリン展開の
有限部分を持っている。この節で、その表現を見ておこう。
そのため、関数 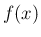 の
の 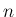 次のマクローリン展開を、便宜的に
と書くことにする。なお、本節も
次のマクローリン展開を、便宜的に
と書くことにする。なお、本節も 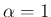 の場合のみを考える。
の場合のみを考える。
まず、巾乗と指数関数の積の (6) には 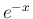 の
マクリーリン展開が含まれていて、
の
マクリーリン展開が含まれていて、
三角関数の 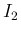 ,
, 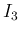 の展開形式の表現は、
(14), (15) から得るか、または
(17) と (19) (と加法定理) から
得ることもできるが、ここでは前者でやってみる。
の展開形式の表現は、
(14), (15) から得るか、または
(17) と (19) (と加法定理) から
得ることもできるが、ここでは前者でやってみる。
まず、(13) より
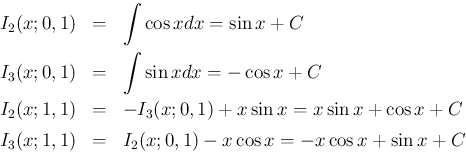
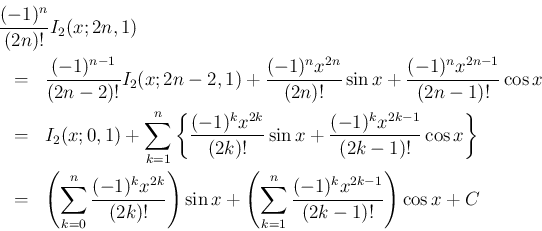
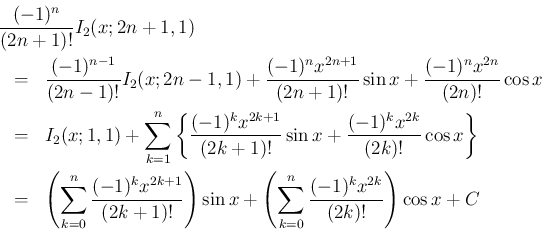
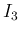 の方は、(14) と (15) より、
の方は、(14) と (15) より、
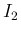 の
の 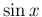 を
を 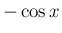 に、
に、
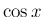 を
を 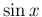 にすればよいので、
にすればよいので、
なぜ、このようなマクローリン展開が含まれるのかを少し考えてみる。
マクローリン展開 ![$[f]_n$](img103.png) の性質として、次の 2 つが容易にわかる。
の性質として、次の 2 つが容易にわかる。
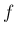 の
の 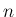 次のマクローリン展開の導関数が、
次のマクローリン展開の導関数が、
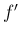 の
の 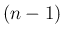 次のマクローリン展開となることを意味している。
次のマクローリン展開となることを意味している。
これらを用いれば、例えば (24) は、右辺を微分すると、
![\begin{eqnarray*}(e^x[e^{-x}]_n)'
&=&
(e^x)'[e^{-x}]_n+e^x([e^{-x}]_n)'
\ =\...
...ght\vert _{x=0} \frac{x^n}{n!}e^x
\ =\
\frac{(-1)^nx^n}{n!}e^x\end{eqnarray*}](img111.png)
![\begin{eqnarray*}\lefteqn{([\cos x]_{2n}\sin x-[\sin x]_{2n-1}\cos x)'}
\\ &=&
...
...n-1})\cos x
%\\ &=&
\ = \
\frac{(-1)^n}{(2n+1)!}x^{2n+1}\cos x\end{eqnarray*}](img112.png)
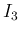 の方も同様に直接これらが成り立つことを証明できる。
の方も同様に直接これらが成り立つことを証明できる。
ただし、これらはあくまで「証明」であって、
マクローリン展開が現われることの説明や理由にはなっていない。
そしてそれを考えていて、もう一つ、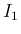 ,
, 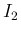 ,
, 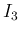 の
計算方法を見つけることができたので、まずそれを以下に紹介する。
の
計算方法を見つけることができたので、まずそれを以下に紹介する。
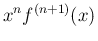 の積分を部分積分すると、
の積分を部分積分すると、
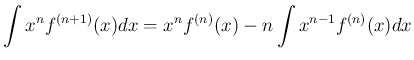
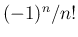 倍すれば
倍すれば
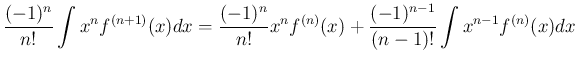
![\begin{eqnarray*}\lefteqn{\frac{(-1)^n}{n!}I_1(x;n,1)
\ =\
\frac{(-1)^n}{n!}\...
...um_{k=0}^n\frac{(-1)^k}{k!}x^ke^x + C}
\\ &=&
e^x[e^{-x}]_n + C\end{eqnarray*}](img118.png)
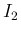 の (25), (26) は
の (25), (26) は
![\begin{eqnarray*}\lefteqn{\frac{(-1)^{n}}{(2n)!}I_2(x;2n,1)
\ =\
\frac{(-1)^{...
...j}\sin x + C
\\ &=&
[\cos x]_{2n}\cos x+[\sin x]_{2n-1}\sin x+C\end{eqnarray*}](img119.png)
ここから考えると、(31) の式は若干マクローリン展開の式に
似てなくもないが、実際には 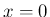 を代入した微分係数も含まれておらず
だいぶ違っていて、
よって
を代入した微分係数も含まれておらず
だいぶ違っていて、
よって 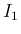 ,
, 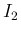 ,
, 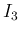 にマクローリン展開が含まれるのは、
にマクローリン展開が含まれるのは、
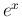 や
や 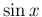 ,
, 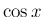 が
が 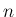 階導関数で
形が変わらないことによる偶然で、たまたまそのような形になっている、
と思われる。
すなわち、
階導関数で
形が変わらないことによる偶然で、たまたまそのような形になっている、
と思われる。
すなわち、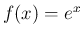 ならば
ならば
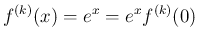
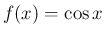 ,
, 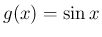 ならば
ならば
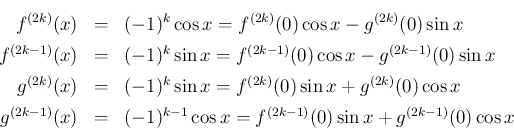
そのことを示す例を一つ紹介する。 部分積分が良く使われる例として、次のようなものもある。
これも、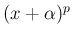 の方を積分する部分積分で
の方を積分する部分積分で 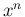 の
次数を一つずつ下げることで積分できるものであるが、
例えば
の
次数を一つずつ下げることで積分できるものであるが、
例えば 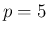 ,
, 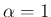 ,
, 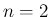 の場合を考えると、
(31) により
の場合を考えると、
(31) により
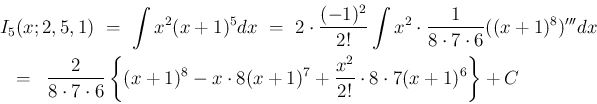
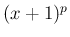 のマクローリン展開は含まれてはいない。
のマクローリン展開は含まれてはいない。
よって (31) の積分結果にマクローリン展開が含まれるのは、
微分によって形が変わらない 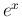 や
や 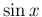 ,
, 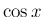 だけに起こる
特別な現象であることがわかる。
だけに起こる
特別な現象であることがわかる。
竹野茂治@新潟工科大学