7 複素数によるつながり
ここまでは、何となく三角関数と双曲線関数の性質が似ていることを見てきたが、
複素数を使えば、直接それらを結びつけることができ、
なぜここまで似た性質を持つのかがわかる。
そのためには、本来は複素関数論をある程度は説明すべきであろうが、
とりあえず必要なのは、オイラーの公式
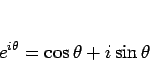 |
(25) |
と、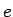 の一般の複素数乗
の一般の複素数乗
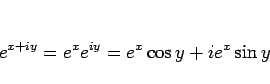 |
(26) |
であるので、これらを認め、複素数乗の指数法則
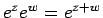 も認めた上で議論を進めることにする。
も認めた上で議論を進めることにする。
(25) を用いると、
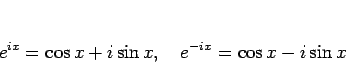
より、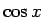 ,
, 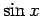 を
を 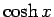 ,
, 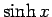 と同様に指数関数で表すことができる。
と同様に指数関数で表すことができる。
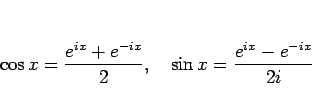
さらにこの式を使って 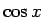 ,
, 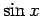 の変数
の変数 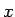 を複素数
を複素数 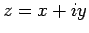 にまで拡張できる。
にまで拡張できる。
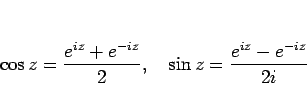 |
(27) |
これが複素関数 (変数も関数値も複素数の関数) としての三角関数の定義である。
同様に複素変数 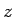 に対する
に対する 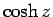 ,
, 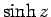 も定義できる。
も定義できる。
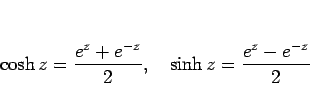 |
(28) |
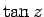 ,
, 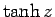 等についても同様である。
そしてこれらの式を用いると、容易に次のことがわかる。
等についても同様である。
そしてこれらの式を用いると、容易に次のことがわかる。
すなわち 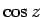 は
は 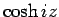 で、
で、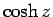 は
は 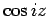 で、
で、
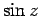 は
は 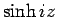 で、
で、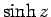 は
は 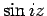 でそれぞれ表されるのである。
複素関数としての三角関数に対しても加法定理は通常と同じ形で成り立つ。
つまり、複素数
でそれぞれ表されるのである。
複素関数としての三角関数に対しても加法定理は通常と同じ形で成り立つ。
つまり、複素数 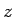 ,
, 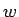 に対して
に対して
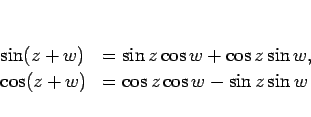 |
(33) |
が成り立つので、
双曲線関数の加法定理が三角関数と似た形になるのはそこからわかる。
すなわち、
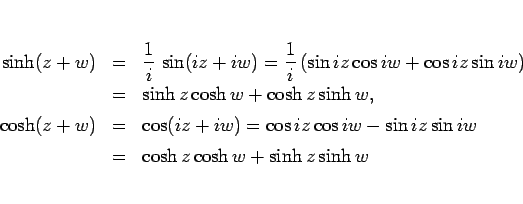
のようになるわけである。
このように考えると、
双曲線関数に関する色んな公式が三角関数と似た形で成り立つのは、
ある程度自然であることがわかる。ちなみに、
初等関数はこのように複素変数で考える方が見通しが良くなることがある。
これを発展させたのが「複素関数論」という分野である。
なお、複素形の三角関数の加法定理 (33) は、
指数法則から成り立つことがわかる。
その計算は、4 節の (9) の証明とほぼ同等であるので省略する。
最後に 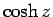 ,
, 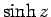 を
を 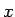 ,
, 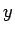 の式で表してみよう。
の式で表してみよう。
なお、これらはこのような展開ではなく、
複素数版の加法定理によって得ることもできる。
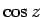 ,
, 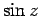 をその方法で同様の形に表してみよう。
それには、加法定理 (33) と、
(29), (31) を用いればよい。
をその方法で同様の形に表してみよう。
それには、加法定理 (33) と、
(29), (31) を用いればよい。
となる。
竹野茂治@新潟工科大学
2010年3月19日
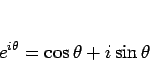
![]() ,
, ![]() を
を ![]() ,
, ![]() の式で表してみよう。
の式で表してみよう。