8 テイラー展開
本節では、双曲線関数のテイラー展開 (マクローリン展開) を紹介する。
良く知られているように、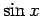 ,
, 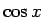 のマクローリン展開は
のマクローリン展開は
となるが、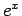 ,
, 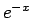 のマクローリン展開は
のマクローリン展開は
であるから、これらを足し引きすれば、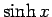 ,
, 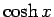 のマクローリン展開
のマクローリン展開
が得られる。
なお、これらは (40), (41) に 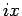 を代入して 7 節の (29), (31) を用いても得ることができる。
を代入して 7 節の (29), (31) を用いても得ることができる。
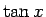 のマクローリン展開は、
微分を使って定義通りに計算するのはかなり面倒なので
例えば以下のように計算すればよい。
のマクローリン展開は、
微分を使って定義通りに計算するのはかなり面倒なので
例えば以下のように計算すればよい。
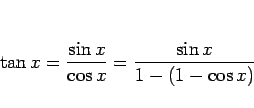
であり、
 では
では
 なので、
なので、
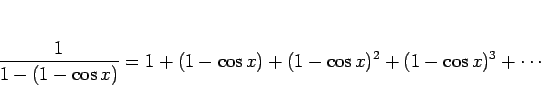
となるから、
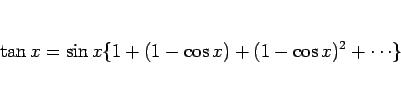
となるが、ここに (40), (41) を代入すれば、
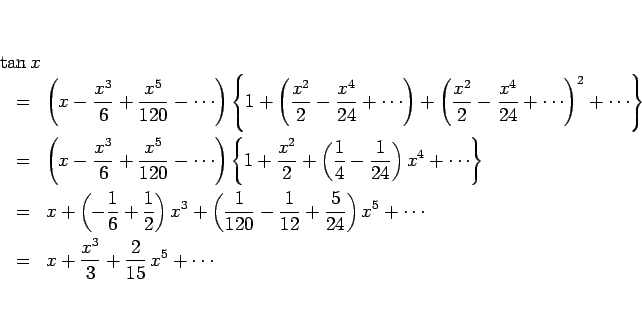
のようになる。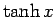 は、(29), (31) より
は、(29), (31) より
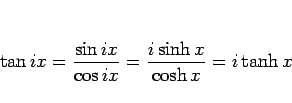
なので、
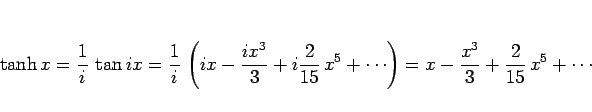
のようにして  の展開式から求めることができる。
の展開式から求めることができる。
次は逆関数のマクローリン展開を考える。
これは、導関数の展開を先に考えると容易に求められる。
例えば  のマクローリン展開は、
のマクローリン展開は、
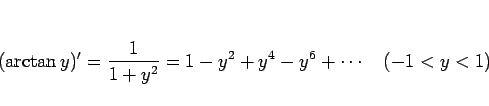
より、この両辺を 0 から 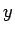 まで積分すれば、
まで積分すれば、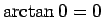 なので、
なので、
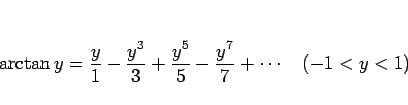 |
(46) |
となる。これと同様にすれば、
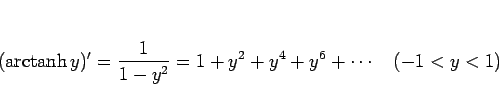
より、
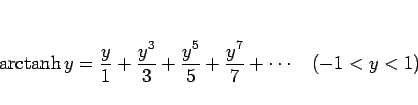 |
(47) |
が得られる。
他の逆関数は、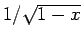 の展開式を利用すればよいが、
一般二項定理により
の展開式を利用すればよいが、
一般二項定理により
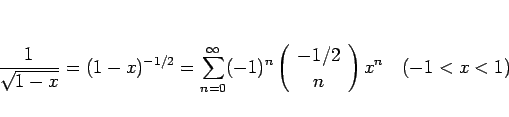 |
(48) |
であり、
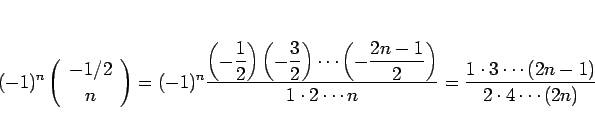
となるが、
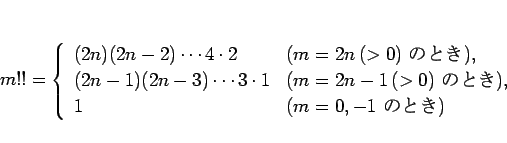
と書くことにすると、結局 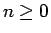 に対して
に対して
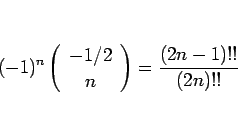
と書けることになり、(48) は、
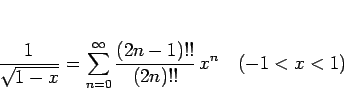 |
(49) |
となる。よって、
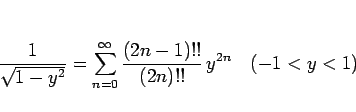
を 0 から 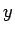 まで積分すれば
まで積分すれば
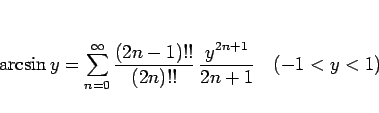 |
(50) |
が得られ、
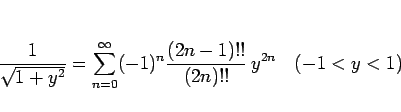
を 0 から 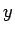 まで積分すれば (17) より
まで積分すれば (17) より
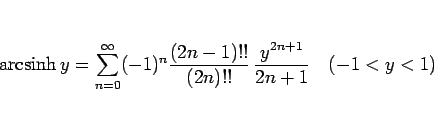 |
(51) |
が得られる。
あとは
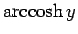 の展開だけであるが、
の展開だけであるが、
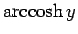 は
は 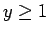 の関数で、
しかも
の関数で、
しかも 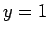 では微分可能ではない (微分係数は
では微分可能ではない (微分係数は 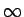 ) のでこのままテイラー展開はできない。
その代わりに
) のでこのままテイラー展開はできない。
その代わりに 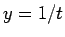 として、
として、
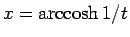 の
の 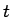 に関する展開を考えてみることにする (
に関する展開を考えてみることにする (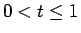 )。
(15) より、
)。
(15) より、
となるが、合成関数の微分 (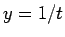 ) と (18) より、
) と (18) より、
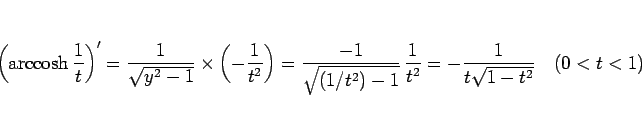
となる。ここで、(49) より
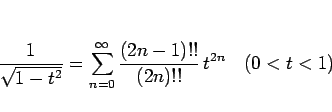
であるから、
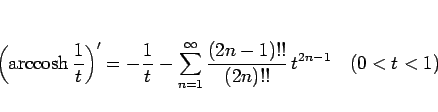
より、
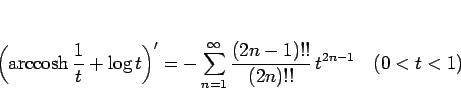
となる。この両辺を 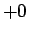 から
から 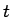 まで積分すると、左辺は
まで積分すると、左辺は
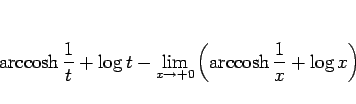
となるが、(52) より
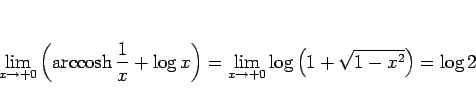
なので、
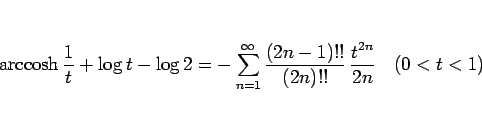
となる。これを 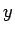 に戻せば、結局
に戻せば、結局
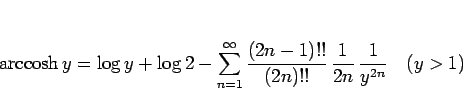 |
(53) |
が得られる。
これは、厳密にはテイラー展開ではないが、
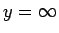 を中心とするようなある種の展開 (漸近展開) になっている。
を中心とするようなある種の展開 (漸近展開) になっている。
竹野茂治@新潟工科大学
2010年3月19日
![]() のマクローリン展開は、
微分を使って定義通りに計算するのはかなり面倒なので
例えば以下のように計算すればよい。
のマクローリン展開は、
微分を使って定義通りに計算するのはかなり面倒なので
例えば以下のように計算すればよい。
![]() のマクローリン展開は、
のマクローリン展開は、
![]() の展開式を利用すればよいが、
一般二項定理により
の展開式を利用すればよいが、
一般二項定理により
![]() の展開だけであるが、
の展開だけであるが、
![]() は
は ![]() の関数で、
しかも
の関数で、
しかも ![]() では微分可能ではない (微分係数は
では微分可能ではない (微分係数は ![]() ) のでこのままテイラー展開はできない。
その代わりに
) のでこのままテイラー展開はできない。
その代わりに ![]() として、
として、
![]() の
の ![]() に関する展開を考えてみることにする (
に関する展開を考えてみることにする (![]() )。
(15) より、
)。
(15) より、