なお、この ![]() の「arc」とは「円弧」のことで、
角度は弧度法では単位円の弧の長さを意味するので、
「三角比
の「arc」とは「円弧」のことで、
角度は弧度法では単位円の弧の長さを意味するので、
「三角比 ![]() に対する弧の長さ」という意味で
に対する弧の長さ」という意味で ![]() のように呼ぶわけである。
のように呼ぶわけである。
もう一つ逆関数を表す流儀として ![]() ,
, ![]() ,
, ![]() の形の記法もよく使われるが、これは
の形の記法もよく使われるが、これは ![]() 乗と紛らわしい (もちろん
乗と紛らわしい (もちろん ![]() と
と ![]() とは全く異なる) ので、本来は使わない方がいいと思うのだが、
基礎数理の教科書 [1] では
とは全く異なる) ので、本来は使わない方がいいと思うのだが、
基礎数理の教科書 [1] では ![]() の記法を採用している1。
の記法を採用している1。
双曲線関数の場合、例えば ![]() は、
は、
![]() から
から
![]() への単調増加関数なので、
定義域を制限せずにそのまま逆関数が作れる。
それを、三角関数の逆関数と同様に
への単調増加関数なので、
定義域を制限せずにそのまま逆関数が作れる。
それを、三角関数の逆関数と同様に
![]() (ハイパボリックアークサイン)、
または
(ハイパボリックアークサイン)、
または
![]() (インバースハイパボリックサイン) と書くようである。
(インバースハイパボリックサイン) と書くようである。
ただし、この「arc」には「弧」の意味はなく、
つまり実際になんらかの曲線の長さを表しているわけではなく、
単に三角関数の逆関数に記号を合わせて「arc」と書いているだけのようである。
実際、
![]() で表される双曲線の
で表される双曲線の ![]() の部分の弧の長さ
の部分の弧の長さ ![]() は、
は、
![]() と
と ![]() は全く同じ関係を意味しているので、
逆関数
は全く同じ関係を意味しているので、
逆関数
![]() のグラフは、単に
のグラフは、単に ![]() の見方を変えて、
横軸と縦軸を入れ換えただけのものになる (図 4)。
の見方を変えて、
横軸と縦軸を入れ換えただけのものになる (図 4)。
![]() の場合は単調ではないので、
の場合は単調ではないので、
![]() に制限して逆関数を考えることになる。
それを
に制限して逆関数を考えることになる。
それを
![]() 、あるいは
、あるいは ![]() と書く (
と書く (![]() )。
)。
![]() は、
は、
![]() 上の単調増加関数であり、
その値域は
上の単調増加関数であり、
その値域は ![]() なので、
逆関数
なので、
逆関数
![]() は
は ![]() 上の関数となる。
上の関数となる。
これらの逆関数は、元々の関数が指数関数の簡単な式で表されるので、
逆関数自体も比較的やさしい式で表すことができる。
例えば、![]() の場合、
の場合、
(14)
![]() の場合も同様で、
の場合も同様で、
(15)
![]() の場合は、
の場合は、
(16)
次に、それぞれの微分を計算してみよう。今求めた (14), (15), (16) を合成関数の微分で計算してもいいのであるが、ここでは逆関数の微分法
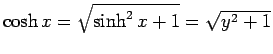 と書けるので、
と書けるので、
(17)
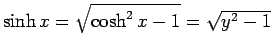 となるので、
となるので、
(18)
(19)
逆にこれらを積分の公式の形に書き直せば、![]() として、
として、
(20)
(21)
(22)
(23)
(24)
これらの公式の大半は ![]() ,
, ![]() などの置換により得られるが、
(21) は、
などの置換により得られるが、
(21) は、![]() の場合は
の場合は ![]() であり、
合成関数の微分により、
であり、
合成関数の微分により、
竹野茂治@新潟工科大学