7 未定係数法
最後に、未定係数法を紹介する。
これは、積分の結果の形を想定して、
積分ではなく微分によって両辺を比較して未定係数を求める、という方法である。
漸化式 (9) によれば、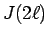 は
は
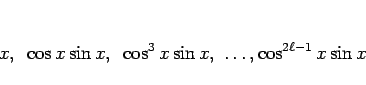
の定数倍の和で表されることがわかる。
よって、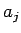 を定数として
を定数として
 |
(19) |
とおいて両辺を微分すると、(8) より
であるから、
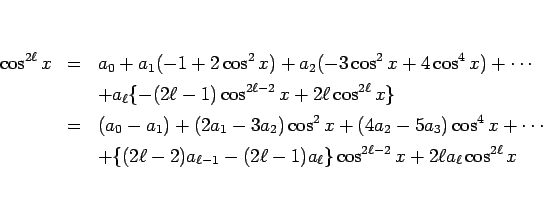
となる。この両辺の 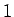 ,
, 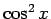 ,
, 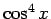 , ...,
, ..., 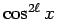 の係数を比較して
の係数を比較して
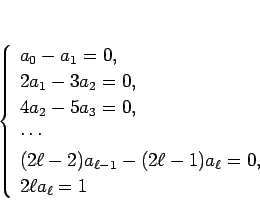
を得る。よって、
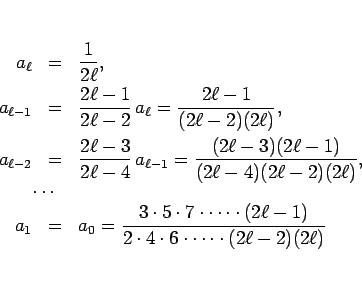
と求まる。一般に 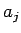 は、
は、
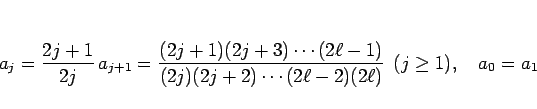
となるから、
これを (19) に代入すれば一般的な公式を作ることもできるが、
具体的な計算では上と同じ計算を行うことで係数を求めるのが良いだろう。
例えば 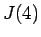 ,
, 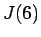 で計算してみる。
で計算してみる。
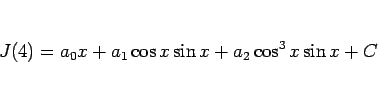
と置いて両辺を微分すれば、
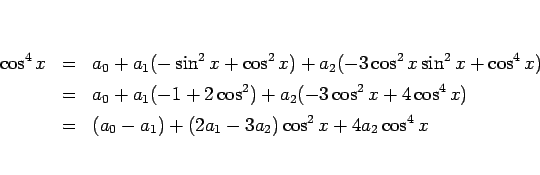
となるので、
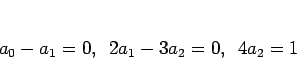
より、
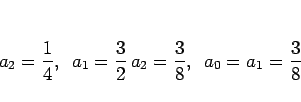
となって、(11) と同じ式が得られることがわかる。
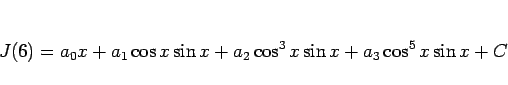
と置いて両辺微分すれば、
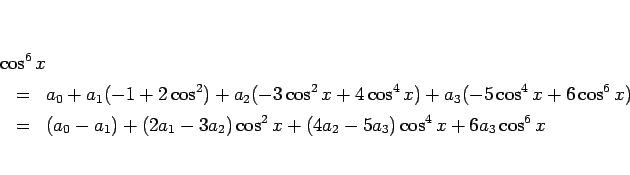
より、
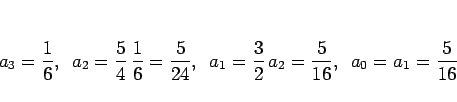
となるから
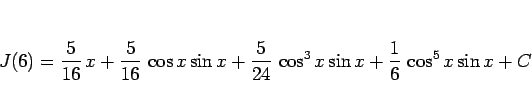
が得られる。
ここでは、(20) を利用したが、
直接計算して変形してもそれほど大変ではない。
ちなみに、これは奇数の方の 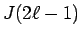 にも使える方法であり、その場合は
にも使える方法であり、その場合は
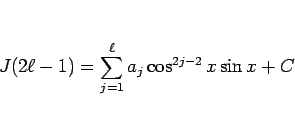
と置いて微分すればよい。
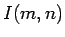 についても、
についても、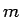 ,
, 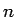 がともに偶数である場合はそれは
がともに偶数である場合はそれは 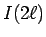 (
(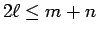 ) の形の和で表されるから、
) の形の和で表されるから、
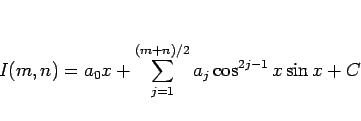
と置いて求めることができる。
ただし、この場合は左辺の微分は
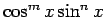 となるので、
これを
となるので、
これを 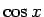 のみの式に変形しないと係数の比較は行えない。
例えば、
のみの式に変形しないと係数の比較は行えない。
例えば、
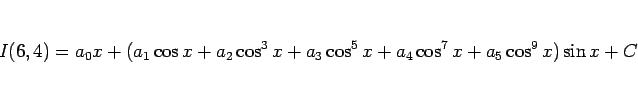
と置いて両辺微分すると
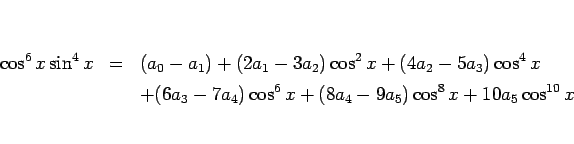
となるが、左辺は
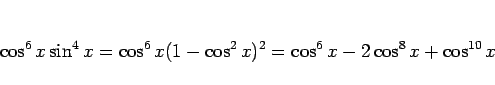
であるから、
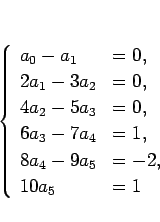
となり、
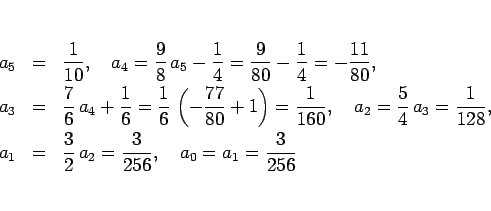
となる。
また、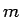 ,
, 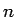 がともに偶数と限らない場合は、
これも 2 節、3 節の議論により、
以下のように置けることがわかる。
がともに偶数と限らない場合は、
これも 2 節、3 節の議論により、
以下のように置けることがわかる。
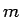 ,
, 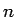 がともに偶数の場合
がともに偶数の場合
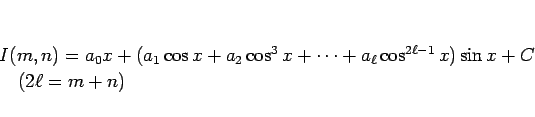
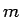 が奇数、
が奇数、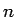 が偶数の場合
が偶数の場合
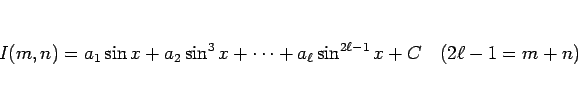
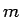 が偶数、
が偶数、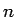 が奇数の場合
が奇数の場合
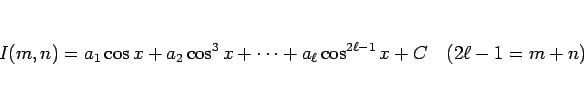
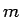 ,
, 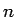 がともに奇数の場合
がともに奇数の場合
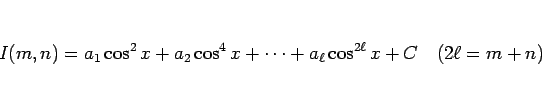
なお、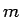 が奇数、
が奇数、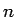 が偶数の場合は上は
が偶数の場合は上は 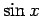 ベースで置いたが、
ベースで置いたが、
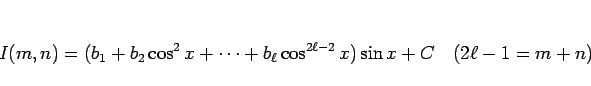
のように置くこともできる。
もちろん、いずれも微分後の左辺も右辺に合わせた形に変形した上で
係数の比較を行わなければいけない。
この未定係数法は、間違いが少なく、
微分さえ得意であればそれほど難しくない良い方法であるが、
積分計算の方法の本筋からはやや外れた方法であり、
またもちろん最終的な形がわからなければ使えないという欠点がある。
その最終的な形を知るためには、
2 節や 3 節の「本筋」の考察が当然必要になる。
だから、本節の微分による計算はむしろ検算に使うことが多い方法だろうと思う。
竹野茂治@新潟工科大学
2010年3月12日
![]() は
は
![]() にも使える方法であり、その場合は
にも使える方法であり、その場合は
![]() についても、
についても、![]() ,
, ![]() がともに偶数である場合はそれは
がともに偶数である場合はそれは ![]() (
(![]() ) の形の和で表されるから、
) の形の和で表されるから、
![]() ,
, ![]() がともに偶数と限らない場合は、
これも 2 節、3 節の議論により、
以下のように置けることがわかる。
がともに偶数と限らない場合は、
これも 2 節、3 節の議論により、
以下のように置けることがわかる。