6 オイラーの公式を利用する方法
4 節の方法も 5 節の方法も、
途中の計算には実は明確な方針はなく、やり方は色々ありうる。
そういう意味で、やや機械的にはやりにくいという点もある。
それを解消するには、複素数を利用して機械的に計算するという方法がある。
そこで利用されるのが以下のオイラーの公式である。
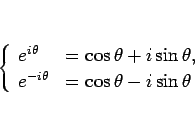 |
(16) |
この公式自体の説明は省略するが、
これを利用すると 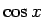 ,
, 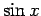 は複素指数を用いて以下のように書ける。
は複素指数を用いて以下のように書ける。
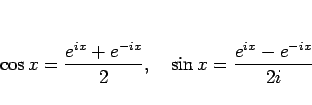 |
(17) |
これを使えば、5 節と同等の 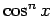 の形の式から
の形の式から 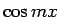 の形の式の和への変形が、
展開と指数法則により機械的に行える。
例えば
の形の式の和への変形が、
展開と指数法則により機械的に行える。
例えば 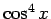 ,
, 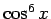 でそれを行ってみる。
でそれを行ってみる。
まず、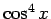 は、
は、
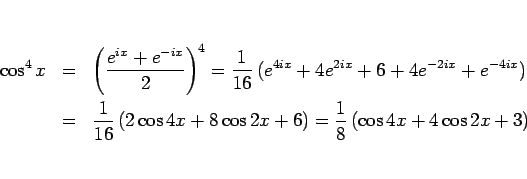
となり、4 乗の二項展開の公式から容易に 4 節の式 (13) と同じ式が得られることになる。
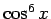 も、
も、
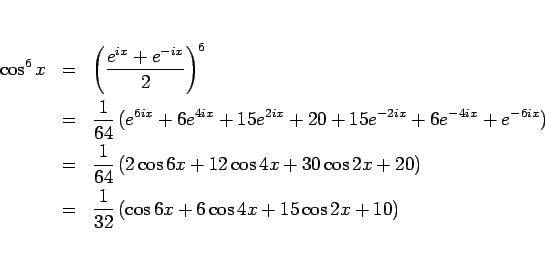
となり、6 乗の二項展開の公式から 5 節の (15) と同じ式が得られる。
これらの例からもわかると思うが、
この方法は三角関数の公式を利用するよりは機械的で計算は楽であるから、
それなりに有用な方法だと思う。
ただし、オイラーの公式 (16) を知らないと使えない方法なので、
実際に基礎数理の講義等でこの方法を導入するのは難しい。
ついでに
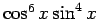 (
(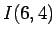 ) の場合も計算してみるが、この場合は、
) の場合も計算してみるが、この場合は、
- 直接 (17) を代入して展開する
- 先に (4) のように
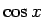 のみの式に変形してから (17) を代入して展開する
のみの式に変形してから (17) を代入して展開する
のような 2 つの方法が考えられるが、前者は展開の計算がやや煩雑であるし、
後者は 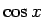 の次数が上がるため、係数の計算がやはりやや面倒になる。
このそれぞれを行ってみる。
の次数が上がるため、係数の計算がやはりやや面倒になる。
このそれぞれを行ってみる。
まずは前者であるが、一応半角の公式
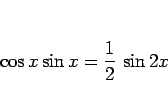
を利用すれば多少は楽になるが、それでも展開はそれなりに煩雑である。
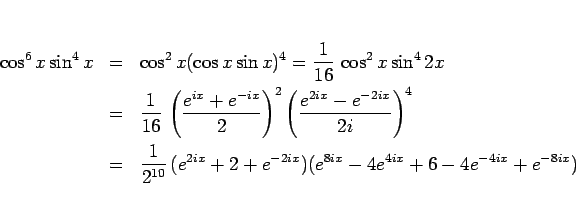
となり、この先の展開がやや面倒で、
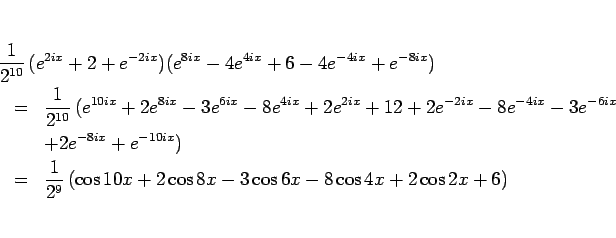
より、
となる。
次に後者の 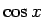 に直してから代入を行う方法で計算してみる。
この場合は積の展開は二項定理を用いるだけなのでその点は難しくない。
に直してから代入を行う方法で計算してみる。
この場合は積の展開は二項定理を用いるだけなのでその点は難しくない。
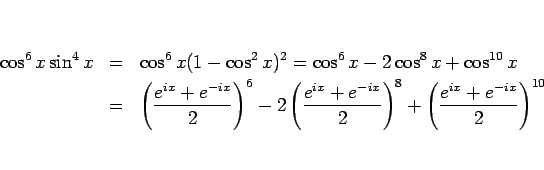
ここで、6 次、8 次、10 次の二項係数は、それぞれ
- 6 次: 1,6,15,20,15,6,1
- 8 次: 1,8,28,56,70,56,28,8,1
- 10 次: 1,10,45,120,210,252,210,120,45,10,1
となるので、
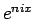 の
の 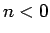 の方は
の方は 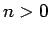 の方と対称であるから省略すれば、
の方と対称であるから省略すれば、
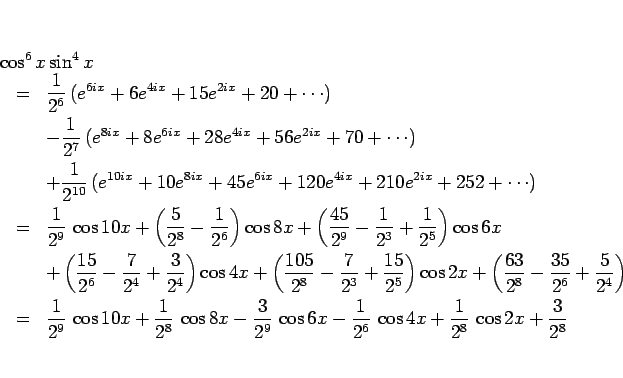
となり、(18) と同じ式が得られる。
こちらは積の展開の計算はないものの、
次数が上がることにより係数が大きくなり、
その係数の計算が大変になることがわかるだろう。
よって、どちらでやっても大差はないが、
大きな数を使わなくて済む分、前者の方が楽かもしれない。
このように、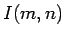 の場合にはこの複素指数を使う方法も、
それほど楽ではないことがわかる。
の場合にはこの複素指数を使う方法も、
それほど楽ではないことがわかる。
竹野茂治@新潟工科大学
2010年3月12日
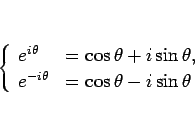
![]() は、
は、
![]() も、
も、
![]() (
(![]() ) の場合も計算してみるが、この場合は、
) の場合も計算してみるが、この場合は、
![]() に直してから代入を行う方法で計算してみる。
この場合は積の展開は二項定理を用いるだけなのでその点は難しくない。
に直してから代入を行う方法で計算してみる。
この場合は積の展開は二項定理を用いるだけなのでその点は難しくない。
![]() の場合にはこの複素指数を使う方法も、
それほど楽ではないことがわかる。
の場合にはこの複素指数を使う方法も、
それほど楽ではないことがわかる。