4 半角の公式で偶数乗を解消する方法
2 節で紹介したように、
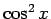 の積分は半角の公式 (3) を用いて積分できる。
一般の偶数乗の場合もこれを必要なだけ繰り返し利用することでそれを解消すれば、
(2) の形か、あるいは奇数乗の形にでき、
奇数乗は 2 節のように置換積分で積分できるので、
これですべての積分を求めることができることになる。
の積分は半角の公式 (3) を用いて積分できる。
一般の偶数乗の場合もこれを必要なだけ繰り返し利用することでそれを解消すれば、
(2) の形か、あるいは奇数乗の形にでき、
奇数乗は 2 節のように置換積分で積分できるので、
これですべての積分を求めることができることになる。
例として、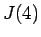 ,
, 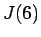 を求めてみる。
を求めてみる。
より、
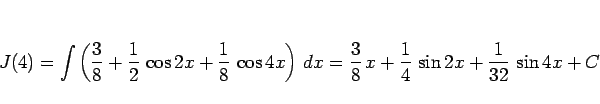
となる。また、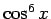 は、
は、
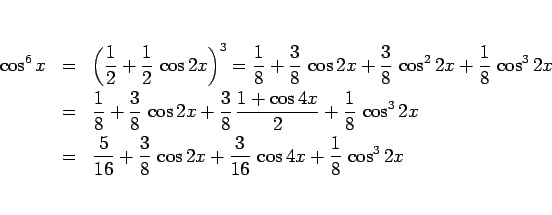
であり、最後の奇数乗の積分には、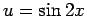 の置換積分を用いる。
の置換積分を用いる。
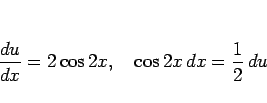
より
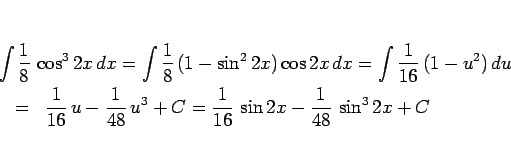
よって、
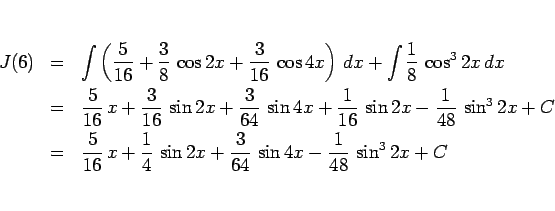
となる。
原理的には、この方法で 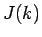 の項はすべて
の項はすべて 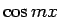 の奇数乗の和の形に直せるので置換積分により積分できることになるが、
途中の計算は煩雑であり、
3 節の部分積分の方法に比べると難しいだろうと思う。
の奇数乗の和の形に直せるので置換積分により積分できることになるが、
途中の計算は煩雑であり、
3 節の部分積分の方法に比べると難しいだろうと思う。
竹野茂治@新潟工科大学
2010年3月12日
![]() ,
, ![]() を求めてみる。
を求めてみる。
![]() の項はすべて
の項はすべて ![]() の奇数乗の和の形に直せるので置換積分により積分できることになるが、
途中の計算は煩雑であり、
3 節の部分積分の方法に比べると難しいだろうと思う。
の奇数乗の和の形に直せるので置換積分により積分できることになるが、
途中の計算は煩雑であり、
3 節の部分積分の方法に比べると難しいだろうと思う。