とし、この fk , gk に対する漸化式を作って、 そこから fk , gk を順に計算する、という方法もある。 漸化式にもいくつかあり、それらをここで紹介し、 計算量の比較などを行ってみる。
-1[Fk] = fk(t),
-1[Gk] = gk(t)
まずは、(4) を利用したものを考える。
であるので、(4) より、
[fk] =
,
[gk] =
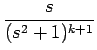
| = | - 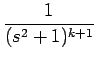 = = 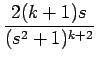 = (2k + 2)Gk+1, = (2k + 2)Gk+1, |
||
| = | - 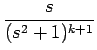 = - = - 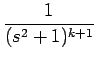 + + 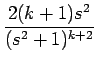 |
||
| = | - Fk + 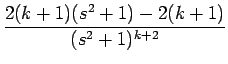 |
||
| = | - Fk +2(k + 1)Fk -2(k + 1)Fk+1 = (2k + 1)Fk - (2k + 2)Fk+1 |
となるので、よって
tfk = (2k + 2)gk+1, tgk = (2k + 1)fk - (2k + 2)fk+1
が得られる。f0 , g0 は、
fk+1 = fk -
gk, gk+1 =
fk
(11)
であるから、(11) を用いて順に、f1 , g1 , f2 , g2 等を計算できる。 なお、(11) の係数の分母を消すために、 この式の両辺に 2k+1(k + 1)! をかけると、
f0 =-1
= sin t, g0 =
-1
= cos t
となるので、
2k+1(k + 1)!fk+1 = (2k + 1)2kk!fk - t2kk!gk, 2k+1(k + 1)!gk+1 = t2kk!fk
となり、(11) より多少式はやさしくなる。
= (2k + 1)
- t
,
= t
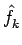
(12)
| = | |||
| = | t |
||
| = | 3 |
||
| = | t |
||
| = | 5 |
||
| = | t |
||
| = | 7 |
||
| = | t |
さらに、(12) から ![]() , あるいは
, あるいは ![]() を
消去して、3 項漸化式を導くこともできる。
(12) より、
を
消去して、3 項漸化式を導くこともできる。
(12) より、
| = | 3 |
||
| = | 5 |
||
| = | 15 sin t - 15t cos t - 6t2sin t + t3cos t, | ||
| = | 7 |
||
| = | 7(15 sin t - 15t cos t - 6t2sin t + t3cos t) - t2(3 sin t - 3t cos t - t2sin t) | ||
| = | 105 sin t - 105t cos t - 45t2sin t + 10t3cos t + t4sin t |
さて、漸化式は (12) 以外にも成り立つ。 例えば、(5) を用いれば、
となるが、k
[fk'] = s
[fk] - fk(0)
なので、
s[fk] = s
=
[gk]
がわかる。同様に (5) より
fk' = gk (k 0)
(15)
となるが、(11) より k
[gk'] = s
[gk] - gk(0)
| s |
= | 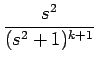 = = 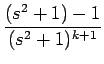 = = 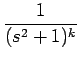 - - 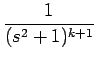 |
|
| = |
が成り立つ。 しかし、この (15) の両辺の添え字は同じであるし、 (16) にも添え字の同じものが含まれているので、 この 2 本から fk , gk を順に計算できる形にはなっていないが、 これらに (11) を組み合わせることで、 一応順に計算できるような形に変形できる。 例えば、(15), (16) に (11) を代入して、
gk' = fk-1 - fk (k 1)
(16)
| fk' | = | ||
| gk' | = | fk-1 - 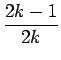 fk-1 + fk-1 + |
を得ることができる。 しかし、この式から fk , gk を計算するには、 積分計算が必要になるが、 そこには tjsin t , tjcos t の形の積分が含まれるので、 必ずしも計算は易しくはない。
= t
,
=
+ t
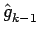
(17)
例えば、
| = | |||
| = | - t cos t + sin t, | ||
| = | |||
| = | t sin t, | ||
| = | |||
| = | |||
| = | - t2sin t + |
||
| = | - t2sin t - 3t cos t + 3 sin t, | ||
| = | |||
| = | - t2cos t + |
||
| = | - t2cos t + t sin t |
最後にもうひとつの漸化式を紹介する。
この
[f]
[g] =
[f * g] =
f (t - y)g(y)dy
![$\displaystyle \left.\vphantom{\int_0^tf(t-y)g(y)dy}\right]$](img249.gif)
(20)
は 畳み込み 演算と呼ばれる。この公式 (20) は、 形式的に以下のように積分の順序交換と置換積分を行うことで得られる:
(f * g)(t) =f (t - y)g(y)dy =
f (y)g(t - y)dy
| = | |||
| = | |||
| = | |||
となるので、畳み込み演算による漸化式
[fk+1] =
[fk * sin t],
[gk+1] =
[gk * sin t]
が得られる。これは一見シンプルでわかりやすいので、 これを漸化式として fk , gk は順次計算できる、 と書いてある本もあるようであるが、 実際にはこれを用いて計算するのもそれほど易しくはない。
fk+1 = fk * sin t, gk+1 = gk * sin t (21)
| f1 | = | f0 * sin t = |
|
| = | 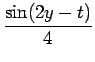 |
||
| = | |||
| f2 | = | f1 * sin t = |
|
| = | |||
| = | 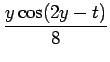 |
||
| = |
結局、漸化式で具体的に fk , gk を求めるには、 (12), または (13), (14) を用いるのが よさそうである。もちろん、(15), (16) や (21) なども全く意味がないわけではなく、 これが使われる場面もちゃんとあるとは思う。
竹野茂治@新潟工科大学