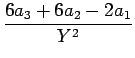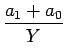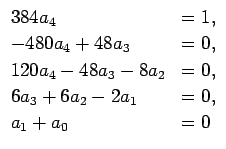8 未定係数法
最後に、未定係数法を用いた計算を紹介する。
これまでの計算からもわかるように、
fk
, gk
は cos t
, sin t
の tj
倍の和の形で表される。
より詳しくは、[2] で紹介したように、
 [tkcos t] = [tkcos t] = 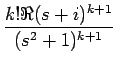 , , 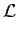 [tksin t] = [tksin t] = 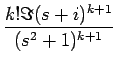
|
(22) |
であり、これらの分子はそれぞれ (k + 1)
次式、k
次式で、
ひとつおきの次数の項しか現れない。よって特に
- 奇関数
t2msin t
,
t2m-1cos t
のラプラス変換は偶関数
- 偶関数
t2mcos t
,
t2m-1sin t
のラプラス変換は奇関数
となる。よって、fk
, gk
は以下のような形に表されることがわかる:
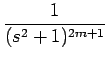 |
= |
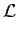 [a2mt2msin t + a2m-1t2m-1cos t + ... + a0sin t], [a2mt2msin t + a2m-1t2m-1cos t + ... + a0sin t], |
|
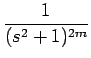 |
= |
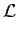 [b2m-1t2m-1cos t + b2m-2t2m-2sin t + ... + b0sin t], [b2m-1t2m-1cos t + b2m-2t2m-2sin t + ... + b0sin t], |
|
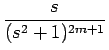 |
= |
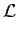 [c2mt2mcos t + c2m-1t2m-1sin t + ... + c0cos t], [c2mt2mcos t + c2m-1t2m-1sin t + ... + c0cos t], |
|
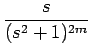 |
= |
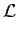 [d2m-1t2m-1sin t + d2m-2t2m-2cos t + ... + d0cos t] [d2m-1t2m-1sin t + d2m-2t2m-2cos t + ... + d0cos t] |
|
未定係数法は、これを利用して aj
, bj
等を未定係数として
代入と比較によりその係数を求める、という方法である。
これなら漸化式のように順に求める必要はなく、fk
, gk
を直接求められる。
例として f4
を考えてみる。
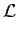 [f4] [f4] |
= |
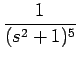 = = 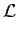 [a4t4sin t + a3t3cos t + a2t2sin t + a1t cos t + a0sin t] [a4t4sin t + a3t3cos t + a2t2sin t + a1t cos t + a0sin t] |
|
| |
= |
a4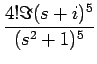 + a3 + a3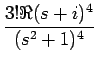 + a2 + a2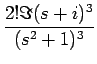 + a1 + a1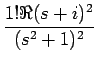 |
|
| |
|
+ a0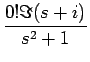 |
|
| |
= |
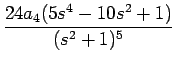 + + 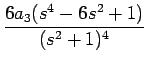 + + 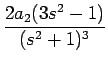 |
|
| |
|
+ 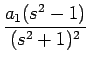 + + 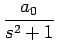 |
|
ここで、Y = s2 + 1
とすると、
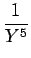 |
= |
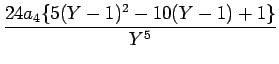 + + 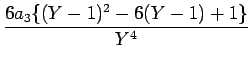 |
|
| |
|
+ 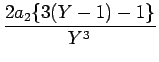 + + 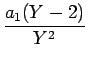 + + 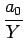 |
|
| |
= |
24a4 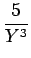 - - 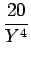 + + 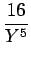  +6a3 +6a3 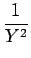 - - 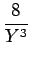 + + 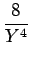  +2a2 +2a2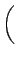 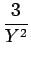 - - 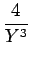  |
|
| |
|
+ a1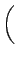 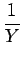 - - 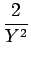  + + 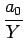 |
|
| |
= |
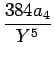 + + 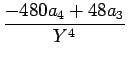 + + 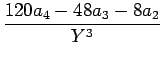 + + 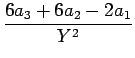 |
|
| |
|
+ 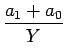 |
|
となるので、この両辺の係数を比較して、
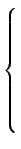 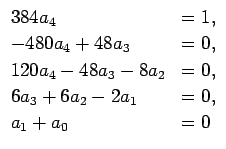
|
(23) |
が得られ、この連立方程式を解けば、
| a4 |
= |
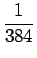 , , |
|
| a3 |
= |
10a4 = 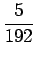 , , |
|
| a2 |
= |
15a4 -6a3 = 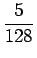 - - 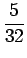 = - = - 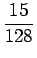 , , |
|
| a1 |
= |
3a3 +3a2 = 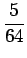 - - 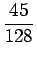 = - = - 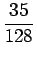 , , |
|
| a0 |
= |
- a1 = 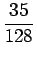 |
|
となるので、よって、
| f4 |
= |
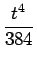 sin t + sin t + 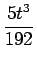 cos t - cos t - 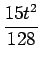 sin t - sin t - 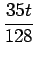 cos t + cos t + 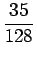 sin t sin t |
|
| |
= |
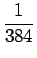 (t4sin t + 10t3cos t - 45t2sin t - 105t cos t + 105 sin t) (t4sin t + 10t3cos t - 45t2sin t - 105t cos t + 105 sin t) |
|
となる。
最後の連立方程式 (23) は、
5 本の方程式なので大変そうに見えるが、
実際には上から順に一つずつ未知数が求まっていくし、
下に行っても未知数の数がそれほど増えないので、
それほど大変ではない。
しかし、そこに至るまでの計算量が多少あるので、
7 節の (13) の計算に比べると、
やや計算量が多いように思う。
竹野茂治@新潟工科大学
2008年3月26日
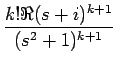 ,
, 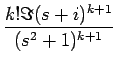
[tkcos t] =
,
[tksin t] =
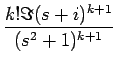
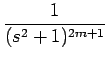
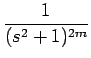
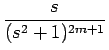
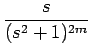
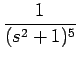 =
= 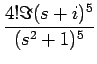 + a3
+ a3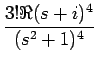 + a2
+ a2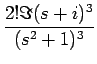 + a1
+ a1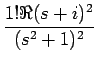
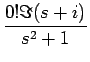
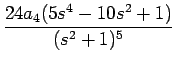 +
+ 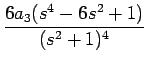 +
+ 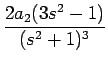
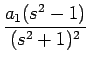 +
+ 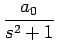
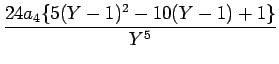 +
+ 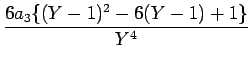
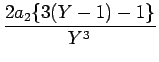 +
+ 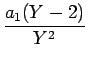 +
+ 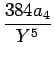 +
+ 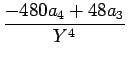 +
+ 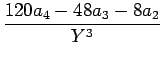 +
+