F(s) = 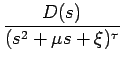 (deg D < 2
(deg D < 2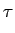 ,
, 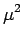 -4
-4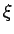 < 0)
< 0)
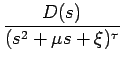 (deg D < 2
(deg D < 2
の形のものを考える。この場合、 s2 +
F(s) =(deg D < 2
,
-4
< 0)
と書き換えることができ、
s2 +s +
= (s - p)2 + q2
p = -
, q =
> 0
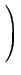
となる。この式で s = p + qS とすれば、
F(s) =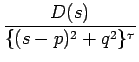
となる。ここで、
F(s) ==
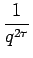
=
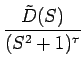
この最後のS に関する式のラプラス逆変換 g(t) が
と求まれば、S = (s - p)/q より、 (3), (6) を用いて変形すれば、
=
[g(t)](S)
| F(s) | = | 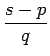 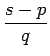 |
|
| = | q |
の形の関数のラプラス逆変換を求めればいいことになる。
(s) =
(deg
< 2
)
(7)
例えば、
の場合を考えると、
F(s) =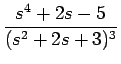
なので、 s + 1 =
F(s) =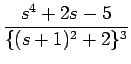
となり、この分子を展開すれば
F(s) =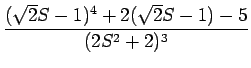
| ( | |||
| = | (4S4 -8 |
||
| = | 4S4 -8 |
||
となる。 これが、
F(s) =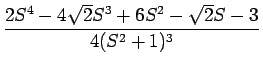
となり、よって、
[g(t)](S) =
[g(t)]
=
[g(
t)](s + 1) =
[
e-tg(
t)](s)
となるわけである。
-1[F] =
e-tg(
t)
(7) をさらに変形して、
よりシンプルな形のものに帰着することもできる。
(7) の分子の
![]() (s)
を
偶数次と奇数次の項に分けて、
(s)
を
偶数次と奇数次の項に分けて、
| = | (b0 + b1s2 + ... + b |
||
| = | D1(s2) + sD2(s2) | ||
| (D1(X)=b0+b1X+ ... +b | |||
| = | 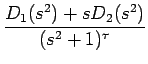 = = 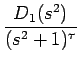 + + 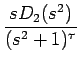 |
||
| = | 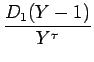 + s + s 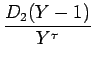 = = 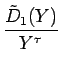 + s + s 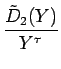 |
||
| = | 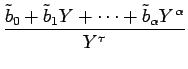 + s + s 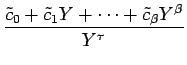 |
||
| = | 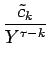 = = 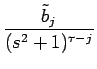 + + 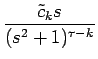 |
の形の関数の逆変換を求めればいいことになる。
Fk(s) = , Gk(s) =
(k
0)
(8)
例えば、前の例で言えば、分子の
2S4 -4![]() S3 +6S2 -
S3 +6S2 - ![]() S - 3
を、奇数次、偶数次に分けて
S - 3
を、奇数次、偶数次に分けて
とし、さらに S2 + 1 = Y を代入して
(2S4 +6S2 -3) - S(4S2 +
)
| {2(Y-1)2+6(Y-1)-3}-S{4 | |||
| = | (2Y2 +2Y - 7) - |
||
| F(s) | = | 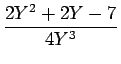 - - 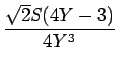 |
|
| = | 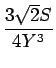 |
||
| = | 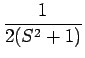 + + 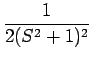 - - 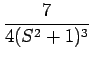 - - 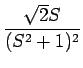 + + 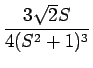 |
よって、以後この Fk(s) , Gk(s) 、 あるいは (7) の形のものの逆変換を考えていくことにする。
竹野茂治@新潟工科大学