![]() を閉区間
を閉区間 ![]() の分割、すなわち、
の分割、すなわち、
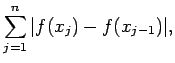 |
(A.117) | |||
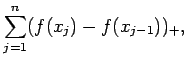 |
(A.118) | |||
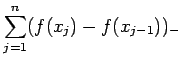 |
(A.119) |
| (A.120) | ||||
| (A.121) | ||||
| (A.122) |
開区間や半開区間 ![]() ,
, ![]() ,
, ![]() (無限区間
(無限区間
![]() ,
, ![]() ,
, ![]() も含む)
に対しては、
も含む)
に対しては、
(A.123)
![]() である関数
である関数 ![]() を、
を、![]() 上の 有界変動関数 と呼ぶ。
上の 有界変動関数 と呼ぶ。
![]() の分割
の分割 ![]() に対して、その
に対して、その ![]() の分点をすべて含む
(よって
の分点をすべて含む
(よって ![]() より細かい)
より細かい) ![]() の分割を
の分割を
![]() の 細分 と呼ぶ。
の 細分 と呼ぶ。
(A.124)
証明
まず、
(A.125)
(A.126)
(A.127)
(A.128)
開区間、半開区間に対しても以下が成り立つ。
![]() のとき、
のとき、
(A.129)
証明
命題 A.1 より、
![]() ならば
ならば
![]() ,
,
![]() となる。よって、任意の
となる。よって、任意の
![]() に対して、
に対して、![]() のある分割
のある分割
![]() ,
, ![]() が存在して、
が存在して、
(A.130)
![]() のとき、
のとき、![]() に対して、
に対して、
証明
前半部分は明らか。後半部分は一般の単調増加関数に対して言える。
今、![]() を
を ![]() 上単調増加な関数であるとすると、
単調収束定理により
上単調増加な関数であるとすると、
単調収束定理により ![]() (端点では片側のみ)
の存在は明らか。よって、不連続点は
(端点では片側のみ)
の存在は明らか。よって、不連続点は
命題 A.3, A.4、および (A.7) より次の系も容易に得られる。
開区間、半開区間 (無限区間も含む) に対しても、 命題 A.3 と同様に以下が成り立つ。
![]() で、かつ
で、かつ
(A.131)
証明
平均値の定理により、任意の分割 ![]() に対し、
に対し、
(A.132)
(A.133)
(A.134)
(A.135)
![]() に対し、
に対し、
(A.136)
証明
![]() の分割
の分割 ![]() ,
, ![]() の分割
の分割 ![]() を取ると、
これを合わせて
を取ると、
これを合わせて ![]() の分割ができる。
これを
の分割ができる。
これを
![]() と書くことにすると、
と書くことにすると、
(A.137)
(A.138)
命題 A.7 より、以下の 2 つの系も容易に得られる
(よって証明は省略する)。
開区間、半開区間に対しても以下が成り立つ。
任意の ![]() と
と ![]() に対して、
に対して、
![]() のとき、任意の
のとき、任意の ![]() に対し、
に対し、
(A.139)
証明
まず、
![]() より、系 A.8
から
より、系 A.8
から
![]() は
は
(A.140)
(A.141)
竹野茂治@新潟工科大学