5.2 L と全変動の関係
この節では、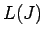 や
や 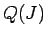 に現れるような波の評価と、
に現れるような波の評価と、
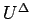 の変動との関係を考える。
の変動との関係を考える。
今、ひとつの Riemann 問題の解
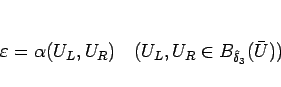
に対し、シュワルツの不等式、および (2.14) により、
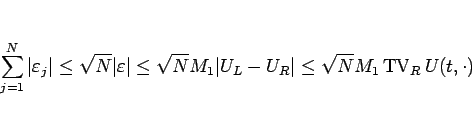 |
(5.54) |
となる。逆に
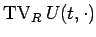 は、
連続波 (膨張波) の変動と不連続波 (衝撃波、および接触不連続) の段差からなり、
は、
連続波 (膨張波) の変動と不連続波 (衝撃波、および接触不連続) の段差からなり、
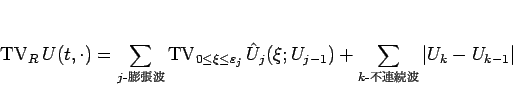 |
(5.55) |
と書けるが、膨張波は 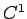 関数であるから、
関数であるから、
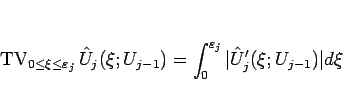
が言え (A 節参照)、
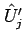 は、(2.13) より
は、(2.13) より
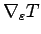 で表現され、
それは (2.15) により
で表現され、
それは (2.15) により 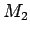 で押さえられるから、
で押さえられるから、
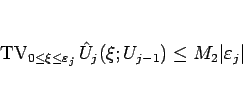 |
(5.56) |
と押さえられることになる。
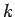 -不連続解に対しても、
-不連続解に対しても、
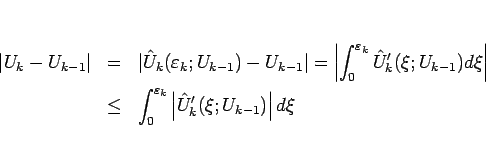
より、
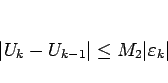 |
(5.57) |
と評価できる。よって、
(5.4), (5.5),
(5.6) により、
Riemann 問題の解 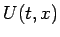 に対して、
に対して、
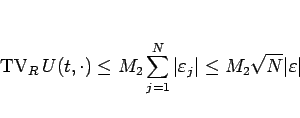 |
(5.58) |
が成り立つ。
(5.3), (5.7) により、
Riemann 問題の解に対し、
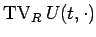 と
と
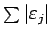 と
と
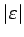 は
同等であることがわかり、
よって、
は
同等であることがわかり、
よって、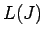 は、
は、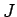 上での
上での 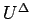 の全変動を評価していることになる。
例えば、
の全変動を評価していることになる。
例えば、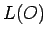 は、(5.3) により
は、(5.3) により
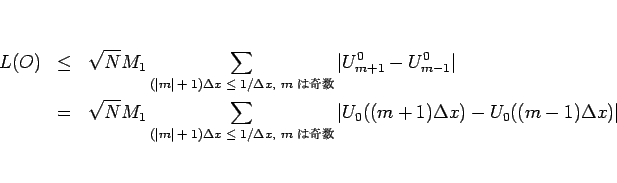
であるので、明らかに
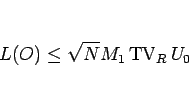 |
(5.59) |
が言える。
竹野茂治@新潟工科大学
2009年1月18日
![]() -不連続解に対しても、
-不連続解に対しても、
![]() と
と
![]() と
と
![]() は
同等であることがわかり、
よって、
は
同等であることがわかり、
よって、![]() は、
は、![]() 上での
上での ![]() の全変動を評価していることになる。
例えば、
の全変動を評価していることになる。
例えば、![]() は、(5.3) により
は、(5.3) により