![]() -曲線 は、左から右に伸びる折れ線で、
-曲線 は、左から右に伸びる折れ線で、
![]() の右隣りの頂点は、
の右隣りの頂点は、![]() か
か ![]() であるものを言う。
なお、
であるものを言う。
なお、![]() に対しては
に対しては
なお、[Glimm], [Smoller] などでは、![]() -曲線には
特にこれ以外の制限を設けてはいないが、
しばらくは
-曲線には
特にこれ以外の制限を設けてはいないが、
しばらくは
![]() (
(![]() ) の
) の
![]() 幅に入り、左右の両方に無限に伸びるもののみを考えるが、
のちほどそれとは別の、特別な
幅に入り、左右の両方に無限に伸びるもののみを考えるが、
のちほどそれとは別の、特別な ![]() -曲線も使う。
-曲線も使う。
![]() -曲線には、
-曲線には、![]() 方向を上と見て自然な半順序関係を考えることができる。
その順序に関する最小元、すなわち
方向を上と見て自然な半順序関係を考えることができる。
その順序に関する最小元、すなわち
![]() の範囲に
一意に決まる
の範囲に
一意に決まる ![]() -曲線を
-曲線を ![]() と書くことにする。
また、1 つの頂点のみが異なる (
と書くことにする。
また、1 つの頂点のみが異なる (![]() と
と ![]() )
) ![]() -曲線の組を、
その大きい方 (
-曲線の組を、
その大きい方 (![]() を持つ方) を、
小さい方 (
を持つ方) を、
小さい方 (![]() を持つ方) に対する直後の
を持つ方) に対する直後の ![]() -曲線 と呼ぶ。
-曲線 と呼ぶ。
![]() -曲線は、近似解の波と交差しながら左から右へ伸びていくが、
その交差する波に関して、次のような汎関数を定める:
-曲線は、近似解の波と交差しながら左から右へ伸びていくが、
その交差する波に関して、次のような汎関数を定める:
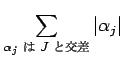 |
(5.52) | |||
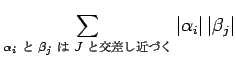 |
(5.53) |
ここで、「交差する波」であるが、
例えば ![]() が膨張波
が膨張波 ![]() の中間にあり、
の中間にあり、
![]() -曲線
-曲線 ![]() は実際にはその膨張波の一部としか交わっていない場合
(図 5.3)、
その交わっている部分
は実際にはその膨張波の一部としか交わっていない場合
(図 5.3)、
その交わっている部分 ![]() の大きさ
の大きさ ![]() のみを
和に加えることとする。
のみを
和に加えることとする。
また、![]() の、
の、![]() と
と ![]() が「近づく」とは、
が「近づく」とは、
![]() が
が ![]() の左にある場合は
の左にある場合は
![]() 、または
、または ![]() で
で ![]() と
と ![]() の
少なくとも一方が衝撃波である場合を言う。
この場合は、波の出発点が離れているもの、
の
少なくとも一方が衝撃波である場合を言う。
この場合は、波の出発点が離れているもの、
![]() が違うものなどもすべて考えることにする。
が違うものなどもすべて考えることにする。
3 節の Glimm 差分の作り方によれば、
![]() -曲線と交わる波は高々有限個であるから
-曲線と交わる波は高々有限個であるから
![]() ,
, ![]() は有限和としてちゃんと定義できる。
また、
は有限和としてちゃんと定義できる。
また、![]() の大きいところには波がなくて
の大きいところには波がなくて ![]() は一定であるから、
そのような波のない場所でのみ異なる
は一定であるから、
そのような波のない場所でのみ異なる ![]() -曲線間の
-曲線間の ![]() ,
, ![]() の値は
それぞれ同じものになる。
その値の意味で考えれば (つまり、波と交わらない部分のみが異なる
の値は
それぞれ同じものになる。
その値の意味で考えれば (つまり、波と交わらない部分のみが異なる ![]() -曲線を
同一視して考えれば)、どの
-曲線を
同一視して考えれば)、どの ![]() -曲線 (
-曲線 (![]() 幅に入るもの) も、
幅に入るもの) も、
![]() から有限個の直後の
から有限個の直後の ![]() -曲線をたどってたどりつくことができることになる。
後で、そのような形での帰納法を用いて評価を求める。
-曲線をたどってたどりつくことができることになる。
後で、そのような形での帰納法を用いて評価を求める。
竹野茂治@新潟工科大学