 の場合」、
および「物理 front 同士の衝突でかつその流入 front の大きさの積が
の場合」、
および「物理 front 同士の衝突でかつその流入 front の大きさの積が
 のとき」に使用する
のとき」に使用する
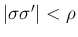 のとき」に使用する
のとき」に使用する
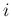 ,
,  ) の
膨張波については、その大きさが
) の
膨張波については、その大きさが 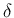 より
大きくても複数の front には分解せず 1 本の front にする
より
大きくても複数の front には分解せず 1 本の front にする
そのために、[1] では p132 で、 accurate method と simplified method をいつ使うか、 そしてさらに accurate method による解の作り方を修正する (P) という要請を 追加している。
 の場合」、
および「物理 front 同士の衝突でかつその流入 front の大きさの積が
の場合」、
および「物理 front 同士の衝突でかつその流入 front の大きさの積が
 のとき」に使用する
のとき」に使用する
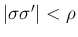 のとき」に使用する
のとき」に使用する
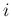 ,
,  ) の
膨張波については、その大きさが
) の
膨張波については、その大きさが 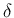 より
大きくても複数の front には分解せず 1 本の front にする
より
大きくても複数の front には分解せず 1 本の front にする
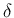 になるように
複数の front に分解することになっているので、
要請 (P) により
になるように
複数の front に分解することになっているので、
要請 (P) により 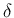 より大きい膨張 front が出る可能性がでてくる。
より大きい膨張 front が出る可能性がでてくる。
そして、この構成法により、p132 と、少し後の話になるが p138 の 7.3 節の 4. で 次のことが言えると述べている。
 の増加方向に一意的に延長可能である
(p132 (P) のすぐ下)
の増加方向に一意的に延長可能である
(p132 (P) のすぐ下)
 でしか使わないから、
(7.57) の評価からすると有限回しか実施しない
(p138)
でしか使わないから、
(7.57) の評価からすると有限回しか実施しない
(p138)
まず 1. であるが、
accurate method では、要請 (P) により流入波と同じ front は
確かに一意的に伸びることになる。
一方、simplified method では、2 通りの場合 (p131 CASE 1, CASE 2) があり、
まず物理 front 同士の衝突の場合は p131 に「(7.25) のように」
Riemann 問題の解から近似解を作る、と書いているが、
「(7.25) のように」ということは、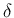 より大きい膨張波が現れれば
それは小さい分解 front に分離することを意味する。
より大きい膨張波が現れれば
それは小さい分解 front に分離することを意味する。
しかし、その直後に
「(7.27) よりそれは、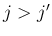 の場合は丁度 2 つの front、
の場合は丁度 2 つの front、
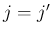 の場合は丁度 1 つの front からなる」と述べている。
これは、膨張波を小さいものに分解しないことを意味するように読める。
下に書かれている図 (Figure 7.7, Figure 7.8) もそれを
説明しているように見えなくもない。
の場合は丁度 1 つの front からなる」と述べている。
これは、膨張波を小さいものに分解しないことを意味するように読める。
下に書かれている図 (Figure 7.7, Figure 7.8) もそれを
説明しているように見えなくもない。
「(7.27)」は、膨張波の分解が起こらないことを意味するのではなく、
Riemann 問題の解が  と
と 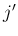 の 2 つの特性族の波しか
出さないことを意味するので、膨張波を分解しない根拠にはならない。
の 2 つの特性族の波しか
出さないことを意味するので、膨張波を分解しない根拠にはならない。
また、要請 (P) は、「accurate method では」と 明確に述べているので、文面上は simplified method には 適用されず、これも分解しない根拠にはならない。
よって分解しない必然性があるとすれば、あとはその大きさが 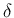 以下
であることだけであるが、逆に要請 (P) は
以下
であることだけであるが、逆に要請 (P) は 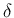 より大きなサイズを
持つ膨張 front を作り得ることを述べていて、
もしそのような膨張 front が存在すれば、
それとサイズの積が
より大きなサイズを
持つ膨張 front を作り得ることを述べていて、
もしそのような膨張 front が存在すれば、
それとサイズの積が 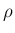 未満になるような小さな衝撃波との衝突が起こすと
それは simplified method で処理され、
それにより
未満になるような小さな衝撃波との衝突が起こすと
それは simplified method で処理され、
それにより 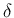 より大きな膨張波が出てしまうことになり、
その分解を止めることはできず、
結局 1. の一意的な延長はできなくなってしまう。
より大きな膨張波が出てしまうことになり、
その分解を止めることはできず、
結局 1. の一意的な延長はできなくなってしまう。
この状況を防ぐには、以下の (Erf) の評価か、別の要請 (P') の いずれかが必要になる。
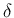 を越えることがないことを示す
を越えることがないことを示す
次は、6. の方であるが、 当然物理 front 接続と非物理 front 接続は 1 度しか交わらないし、 特性族の異なる物理 front 接続同士も 1 度しか交わらないことはわかる。 問題は、同じ特性族の物理 front 接続同士が、2 度以上交わることはないか、 という点である。
衝突したときに accurate method が行われるのであれば、 (P) によりそれは 1 つの特性族には 1 本の front として 合体した形で延長されるので、当然それ以上の衝突は発生しない。 一方 simplified method が行われる場合は、 「(P') の保証があれば」accurate method 同様 1 つの特性族には 1 本の front になるが、 もし (P') の保証がなければ複数の分解 front に分離する可能性がある。
つまり、この 6. に関しても 1. と同様の問題があり、 やはり (P') が必要となるので、 本稿では (P') を仮定して話をすすめることにする。
なお、その (P), (P') の要請、および後
(3.6 節と 6 節) で述べる
速度変化の制限の仮定の元、
それを満たす近似解が作れていれば、
上の 1.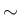 7. が確かに成り立ち、よって衝突時刻も有限個となり、
大きさに関する a priori 評価さえあれば、
近似解は有限の時間内で無限回の衝突を起こすことはなく、
無限時刻にまで近似解を伸ばせることがわかる。
7. が確かに成り立ち、よって衝突時刻も有限個となり、
大きさに関する a priori 評価さえあれば、
近似解は有限の時間内で無限回の衝突を起こすことはなく、
無限時刻にまで近似解を伸ばせることがわかる。
竹野茂治@新潟工科大学