 の増加方向に一意的に延長可能である」とあり (p132)、
そしてそのように延長したものを「wave front」と呼んでいるように
読める箇所もある。
の増加方向に一意的に延長可能である」とあり (p132)、
そしてそのように延長したものを「wave front」と呼んでいるように
読める箇所もある。
[1] では、 wave front, shock front, rarefaction front, non-phisical front といった 用語が p125 の Definition 7.1 あたりから出てくるが、 その「front」という用語の明確な定義がなく、 「wave」(shock wave 等) とほぼ同様の意味で使っているように思える。
ただし、[1] による近似解では微小な速度の変更を 行うことがあるので、 厳密な意味では各不連続波はいわゆる「shock wave」(衝撃波) ではないし、 「rarefaction wave」(膨張波) ではない。 その意味で近似解の方の不連続波を「front」を呼んでいるのかもしれないが、 それも明確ではない。
また、[1] の場合 p132 の近似解の作り方により、
1 本の wave front は、他の front との相互作用で丁度その大きさが 0 に
なって消えてしまうまでは
「 の増加方向に一意的に延長可能である」とあり (p132)、
そしてそのように延長したものを「wave front」と呼んでいるように
読める箇所もある。
の増加方向に一意的に延長可能である」とあり (p132)、
そしてそのように延長したものを「wave front」と呼んでいるように
読める箇所もある。
一方、[5] では明確に front を定義していて (p210)、 「wave」と「front」の区別もつけている。 ただ、[5] の作り方では 一意的に延長することは不可能なので、[1] のような 呼び方はしておらず、[1] の用語を知るための参考にはならない。
よって、本稿では、とりあえず次のような使い分けを行っておく。
なお、[5] では、
「front とは一つのオブジェクトであり、L, R とラベル付けされる 左右の定数状態、および特性族を持つ」とあるが、本稿では、個々の front は、
左右の定数状態、特性族、位置 (線分の方程式と出発点、終了点)、 大きさ、および移動速度を持つオブジェクトと考えることにする。当然、wave も同様の属性値を持つオブジェクトとなる。 なお、上記の属性値はすべてが独立というわけではなく、 例えば物理 front であれば、 特性族と大きさと左の定数状態から右の定数状態は決定するし、 移動速度は、若干の変更がありうるものの、左右の定数状態と特性族と 大きさからある程度の値は決定する。 また、出発点は必ず存在するが、終了点は無限の先になる場合もあり得る。
[1] は、個々の front を記号づけすることはしておらず、
数式では主にその大きさのみを 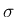 の記号で表現するのみである。
p138 以降では、個々の front (接続) に
の記号で表現するのみである。
p138 以降では、個々の front (接続) に 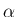 という添字をつけ、
その front (接続) の大きさを
という添字をつけ、
その front (接続) の大きさを
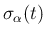 のように
呼ぶ工夫はしているが、直接 front (接続) を指す記号は導入していない。
一方 [5] は、通常は大きさを表す
のように
呼ぶ工夫はしているが、直接 front (接続) を指す記号は導入していない。
一方 [5] は、通常は大きさを表す 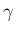 のようなものも front と
呼んでいて、これは逆に
のようなものも front と
呼んでいて、これは逆に 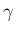 をオブジェクトとしての front を表す
名称と見れば、それが文脈によりその属性値である大きさも意味することもある、
と見ることもできる。
をオブジェクトとしての front を表す
名称と見れば、それが文脈によりその属性値である大きさも意味することもある、
と見ることもできる。
これは、例えば線分というオブジェクトを意味する AB という記号が、
「AB=3」のように文脈によりその長さという属性値を意味することが
あるのと同様の使い方であり、
よって本稿でもそのように使うことにして、
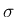 をオブジェクトとしての front を指す記号とし、
文脈によりその
をオブジェクトとしての front を指す記号とし、
文脈によりその 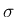 を大きさを意味するスカラー値と見たり、
後で導入する
を大きさを意味するスカラー値と見たり、
後で導入する  のように、
のように、
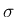 をオブジェクトとしての front 自身を意味することもある、
とする。
をオブジェクトとしての front 自身を意味することもある、
とする。
竹野茂治@新潟工科大学