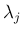 」である。
通常、保存則の論文等では「
」である。
通常、保存則の論文等では「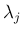 」は、
」は、 の
の  番目の
固有値
番目の
固有値 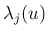 としてしか使われないが、
この [1] では以下の 3 種類の意味で使用されている。
としてしか使われないが、
この [1] では以下の 3 種類の意味で使用されている。
その 1 つ目は「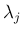 」である。
通常、保存則の論文等では「
」である。
通常、保存則の論文等では「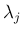 」は、
」は、 の
の  番目の
固有値
番目の
固有値 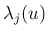 としてしか使われないが、
この [1] では以下の 3 種類の意味で使用されている。
としてしか使われないが、
この [1] では以下の 3 種類の意味で使用されている。
 の固有値
の固有値 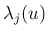 (p90:
(p90: 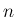 変数
変数  の実数値関数)
の実数値関数)
 -衝撃波 (または接触不連続) 速度
-衝撃波 (または接触不連続) 速度
 (p124:
(p124:
 ,
, 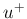 で決まるが、
で決まるが、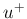 の取り得る値は
の取り得る値は  によって
決まる 1 次元曲線上なので、
によって
決まる 1 次元曲線上なので、
 ,
, 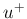 の
の  変数関数ではない。通常は
変数関数ではない。通常は 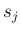 と書かれる)
と書かれる)
 -衝撃波 (または接触不連続) 速度
-衝撃波 (または接触不連続) 速度
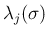 (p93: 一つの 1 次元パラメータ
(p93: 一つの 1 次元パラメータ 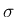 の 1 変数実数値関数)
の 1 変数実数値関数)

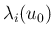 」は固有値、
次の「
」は固有値、
次の「
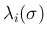 」は上の 3 つ目のもの、
後ろの 2 つはまた固有値、となっていて、
同じ
」は上の 3 つ目のもの、
後ろの 2 つはまた固有値、となっていて、
同じ 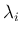 という記号が、
一つの式の中で 2 つの意味で使われていることになる。
このような例が、p93, p96 下などにも見られるし、
7 章でも p124 などに見られる。
という記号が、
一つの式の中で 2 つの意味で使われていることになる。
このような例が、p93, p96 下などにも見られるし、
7 章でも p124 などに見られる。
これは、[1] の筆者には便利なのかもしれないが、
読者にはあまりわかりやすいものではなく、
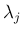 を見るたびにそれがどの意味かを
確認しなければいけない。
本来は、2 つ目は
を見るたびにそれがどの意味かを
確認しなければいけない。
本来は、2 つ目は 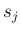 , 3 つ目もそれを使うのであれば
別の記号 (例えば
, 3 つ目もそれを使うのであれば
別の記号 (例えば 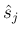 ) を使うべきだろうと思う。
) を使うべきだろうと思う。
もうひとつ [1] の 2 つ目の気になる記号として、
固有ベクトルの「 」がある。
これは、「記号を変えずに意味だけ書き換える」ことがされているのであるが、
Bressan は自著、論文でよく同様のことを行っている
ようである (そして、そのために当初の目標と結果がずれてしまっている
論文もある)。
」がある。
これは、「記号を変えずに意味だけ書き換える」ことがされているのであるが、
Bressan は自著、論文でよく同様のことを行っている
ようである (そして、そのために当初の目標と結果がずれてしまっている
論文もある)。
固有ベクトルは、5 章 (p90) の定義 5.1 で定義されていて、
ここでは固有ベクトル  は単位ベクトルとして定義されている。
固有べクトルの向きは、真性非線形の場合は (5.5) (p91) のように取るとして、
これで真性非線形の特性方向の固有ベクトルは一つに決まることになる。
なお、線形退化の場合は
は単位ベクトルとして定義されている。
固有べクトルの向きは、真性非線形の場合は (5.5) (p91) のように取るとして、
これで真性非線形の特性方向の固有ベクトルは一つに決まることになる。
なお、線形退化の場合は  の向きは決定せず、2 通りがありうる。
の向きは決定せず、2 通りがありうる。
ところが、5.2 節 (p98) で、真性非線形の場合は
「として、と正規化できる」
 固有ベクトルを同じ記号のまま、
単位ベクトルであることを捨てて上の条件を満たすものに
書き換えているのであるが、これは混乱を生みかねないと思う。
むしろ本来は
固有ベクトルを同じ記号のまま、
単位ベクトルであることを捨てて上の条件を満たすものに
書き換えているのであるが、これは混乱を生みかねないと思う。
むしろ本来は
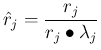
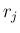 の単位ベクトルの定義の方は (5.4) とちゃんと式番号が
振られているのであるが、
その後の正規化の式には式番号が振られておらず
文章中に埋もれているため、あまり探しやすくもない。
そのため、より混乱が起きやすくなっているように感じる。
の単位ベクトルの定義の方は (5.4) とちゃんと式番号が
振られているのであるが、
その後の正規化の式には式番号が振られておらず
文章中に埋もれているため、あまり探しやすくもない。
そのため、より混乱が起きやすくなっているように感じる。
また、当然線形退化の特性方向の場合は
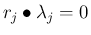 だから
このような正規化はできず、その場合
だから
このような正規化はできず、その場合 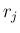 は単位ベクトルのままである。
その意味でも、本来はちゃんと記号を書き分けるべきであろうと思う。
は単位ベクトルのままである。
その意味でも、本来はちゃんと記号を書き分けるべきであろうと思う。
なお、波面追跡法の本論の 7 章では固有ベクトル 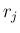 はほとんど
出てこないので、その点ではこれに関する実害はほとんどない。
はほとんど
出てこないので、その点ではこれに関する実害はほとんどない。
竹野茂治@新潟工科大学