
 は
は 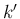 ,
, 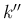 の
小さい方の世代で、
の
小さい方の世代で、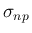 は少なくとも
は少なくとも 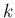 以上の世代となる。
以上の世代となる。
よって、
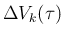 の方は (54) より
の方は (54) より
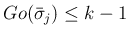 なので、
なので、

 の方は、[A-2] 同様に
の方は、[A-2] 同様に
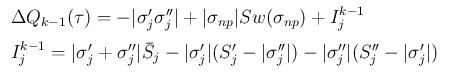
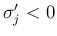 ,
, 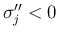 の場合は、
(55) より
の場合は、
(55) より
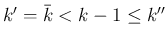 なら
なら
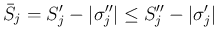
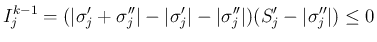
 の場合は
の場合は 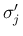 と
と  等が
入れかわるだけ。
等が
入れかわるだけ。
3. の 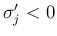 ,
, 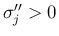 ,
,
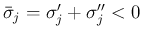 の場合は、
の場合は、
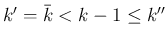 なら
なら
 で、
で、
 なら
なら
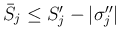 なので、
いずれの場合も
なので、
いずれの場合も

4. の 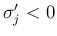 ,
, 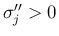 ,
,
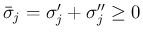 の場合、
の場合、
 ならば当然
ならば当然
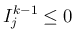 なので
なので
 とすると、
とすると、
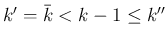 なら
なら
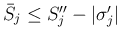 ,
,
 なら
なら
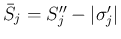 なので、
いずれの場合も
なので、
いずれの場合も
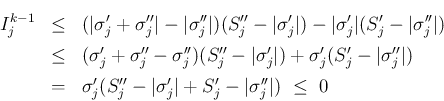
よっていずれの場合もすべて
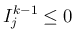 となり、
となり、
竹野茂治@新潟工科大学