3.8
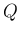 の評価: [S-2] の場合
の評価: [S-2] の場合
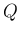 の評価: [S-2] の場合
の評価: [S-2] の場合
3.6 節で述べたように、
接触不連続 front 同士はぶつからないとしているので、この場合は真性非線形で、
よって
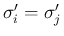 と
と  の少なくとも一方は
衝撃 front であり、
の少なくとも一方は
衝撃 front であり、
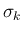 は、
は、
 と
と 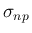 となる。
これも
となる。
これも 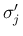 ,
,  ,
,
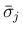 の符号で場合分けすれば、
3.6 節の 1. から 6. までのうち 2. を
除く 5 通りとなる。1. の場合は、
の符号で場合分けすれば、
3.6 節の 1. から 6. までのうち 2. を
除く 5 通りとなる。1. の場合は、

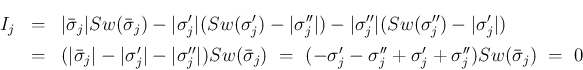

同様に、4. で
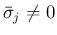 の場合は
の場合は
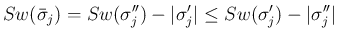
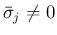 の場合は
の場合は
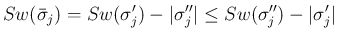
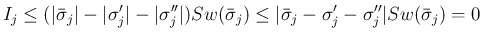
 の場合も当然
の場合も当然  となるので、
いずれの場合も 1. の場合と同様にして (7.56') が得られる。
となるので、
いずれの場合も 1. の場合と同様にして (7.56') が得られる。
3. の場合は
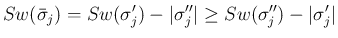

5. の場合も 3. の 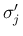 と
と  を入れかえるだけなので、
(7.56') が成り立つことがわかる。
を入れかえるだけなので、
(7.56') が成り立つことがわかる。
竹野茂治@新潟工科大学