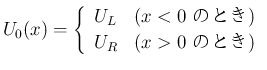 (24)
(24)
方程式 (2) に、原点で段差を持つ階段関数の初期値
を与えた問題を Riemann 問題 と呼ぶ。これは、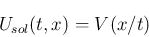
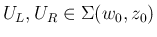 に対し、
に対し、
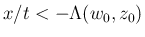 ならば
ならば
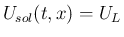 ,
,
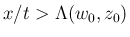 ならば
ならば
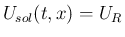 ,
,
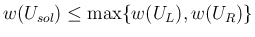 ,
,
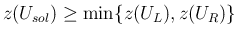
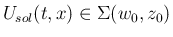 であることもわかる。
であることもわかる。
さらに、方程式 (2) は発散形で、
不連続線上では Rankine-Hugoniot 条件を満たすので、CFL 条件
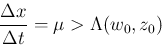
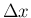 ,
, 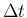 に対し、
に対し、
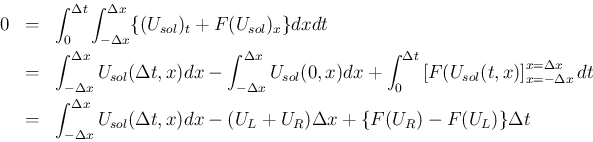
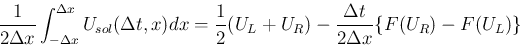
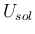 の
の 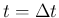 上の
上の
![$[-\Delta x,\Delta x]$](img172.png) での積分平均が
での積分平均が 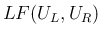 となる。
となる。
が
上の、区間
に値を取る実数値関数で、
が区間
上で下に凸ならば、
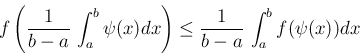
が区間
上で上に凸ならば、
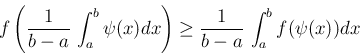
今、
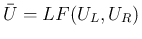 とすると、
(25) と命題 1、
命題 4、
および
とすると、
(25) と命題 1、
命題 4、
および
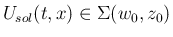 により、
により、
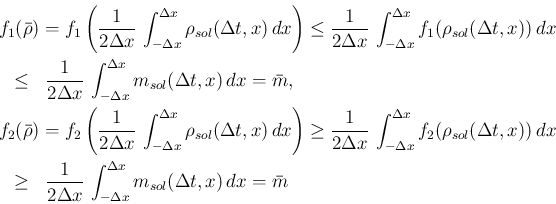
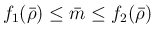 と
なるので、命題 1 より
と
なるので、命題 1 より
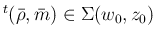 が
言えることになる。
これが、定理 2 の通常の証明の流れである。
が
言えることになる。
これが、定理 2 の通常の証明の流れである。
竹野茂治@新潟工科大学