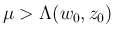 (21)
(21)
CFL 条件
の元で、ならば、
, すなわち、
が成り立つ (この意味で、は、LF 差分に 対する 不変領域 と呼ばれる)。
なお、この定理 2 は、次の仮説 3 よりも やや条件が強いことに注意せよ。
CFL 条件 (12) () の元で、
が成り立つ。もし、仮説 3 が成り立てば、 定理 2 はそれにより示される。 それは、
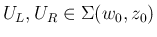 で (21) が
満たされていれば、
で (21) が
満たされていれば、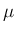 は当然 (12) を満たすので、
(23) が成り立つことになり、
は当然 (12) を満たすので、
(23) が成り立つことになり、
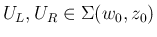 から (22) が得られる。
から (22) が得られる。
しかし、この逆、すなわち定理 2 から
仮説 3 は一般には得られない。
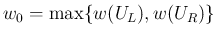 ,
,
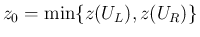 とすればいいように思うかもしれないが、
例えば
とすればいいように思うかもしれないが、
例えば
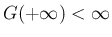 の場合は、
まずその
の場合は、
まずその 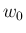 ,
, 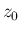 に対応する
に対応する 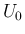 が存在するとは限らない。
実際、
が存在するとは限らない。
実際、
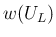 に対して、
に対して、
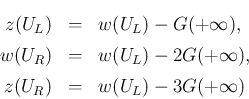
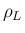 ,
, 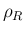 は、
は、
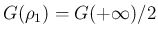 なる
なる 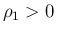 に対して
に対して
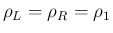 と
なり、
と
なり、
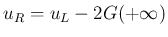 より
より 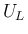 ,
, 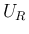 はちゃんと存在するが、
はちゃんと存在するが、
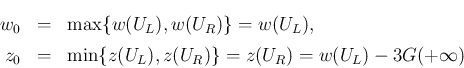
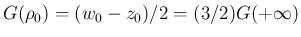 となるが、
そのような
となるが、
そのような 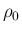 は存在しない。
は存在しない。
また、その 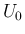 が存在したとしても、
仮説 3 の仮定として満たすべき CFL 条件 (12) から、
定理 2 で必要な CFL 条件 (21) が
得られるとは限らない。
それは、一般には
が存在したとしても、
仮説 3 の仮定として満たすべき CFL 条件 (12) から、
定理 2 で必要な CFL 条件 (21) が
得られるとは限らない。
それは、一般には
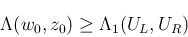
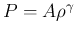 (
(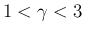 ) の場合でも、
) の場合でも、
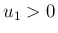 ,
, 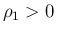 に対して、
に対して、
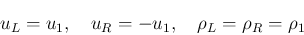
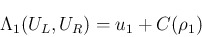
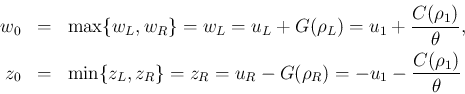
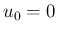 で、
で、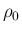 は
は
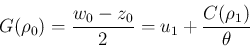
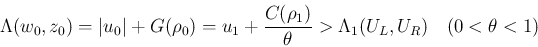
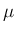 がその間に入ってしまうと
定理 2 からは何も言えなくなってしまう。
がその間に入ってしまうと
定理 2 からは何も言えなくなってしまう。
よって今回は、仮説 3 ではなく、 少し強い CFL 条件 (21) を仮定に置く 定理 2 について考察する。 なお、仮説 3 が実際に成立するか、 それとも反例があるかはよくわからない。
竹野茂治@新潟工科大学