4 とりあえず N 回やる場合
次は、3. の、あたってもはずれても
とりあえず 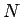 回までやり続ける場合を考える。
回までやり続ける場合を考える。
毎回のくじは独立であるから、この場合の期待値は明らかに
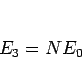 |
(11) |
であるが、ここでは別の計算方法を紹介する。
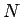 回のうち、
回のうち、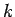 回があたり、
回があたり、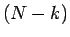 回がはずれとなる組み合わせは
回がはずれとなる組み合わせは
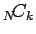 通りあり、
それぞれが
通りあり、
それぞれが 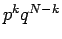 の確率で起こり、
そしてこのとき
の確率で起こり、
そしてこのとき 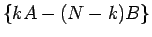 円もらえるので、
これを
円もらえるので、
これを 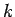 に関して
に関して 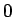 から
から 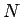 まで加えると、
まで加えると、
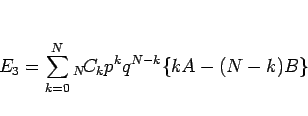 |
(12) |
となる。このような和を計算するのに必要となる計算式を紹介する。
一つは二項展開定理:
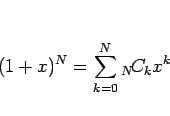 |
(13) |
であり、もうひとつはこの (13) を 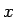 で微分して
で微分して
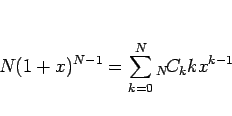
さらに 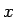 倍して得られる次の式である:
倍して得られる次の式である:
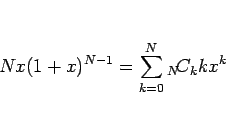 |
(14) |
(12) を、これらが使える形に変形する。
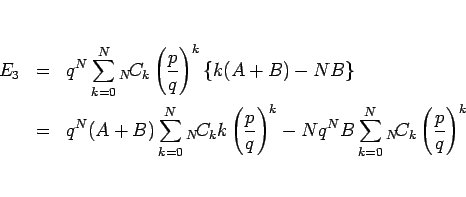
となるので、(13), (14) より、
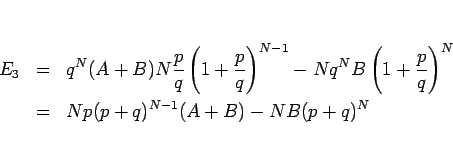
となるが、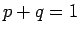 なので、
なので、
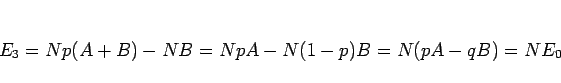
となり、(11) に一致する。
竹野茂治@新潟工科大学
2007年4月28日
![]() 回のうち、
回のうち、![]() 回があたり、
回があたり、![]() 回がはずれとなる組み合わせは
回がはずれとなる組み合わせは
![]() 通りあり、
それぞれが
通りあり、
それぞれが ![]() の確率で起こり、
そしてこのとき
の確率で起こり、
そしてこのとき ![]() 円もらえるので、
これを
円もらえるので、
これを ![]() に関して
に関して ![]() から
から ![]() まで加えると、
まで加えると、