3 あたるか N 回までやり続ける場合
次は、2. の、あたるか 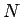 回までやり続ける場合を考える。
回までやり続ける場合を考える。
この場合の期待値 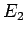 は、(2) に代わり
は、(2) に代わり
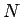 回目までの有限和となるが、
回目までの有限和となるが、
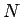 回目がはずれた場合の項も追加される。よって
回目がはずれた場合の項も追加される。よって 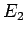 は、
は、
となる。今、
とすると、
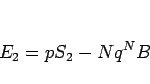 |
(8) |
であり、(7) の両辺を 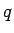 倍すると、
倍すると、
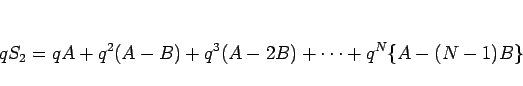 |
(9) |
となるので、(7), (9) の差を取れば、
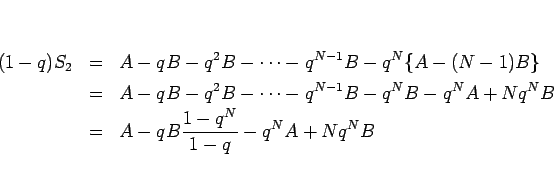
となる。よって、
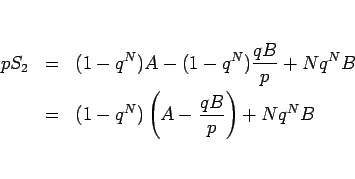
となるので、(8) より
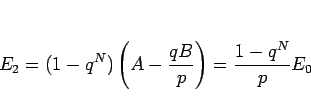 |
(10) |
が得られる。
竹野茂治@新潟工科大学
2007年4月28日
![]() は、(2) に代わり
は、(2) に代わり
![]() 回目までの有限和となるが、
回目までの有限和となるが、
![]() 回目がはずれた場合の項も追加される。よって
回目がはずれた場合の項も追加される。よって ![]() は、
は、