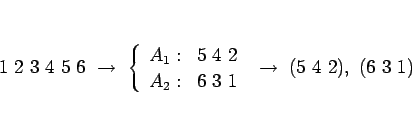
���ξ�硢1 ��μ��Ǥϡ�5 ���
�Ҥ٤��ΤȤϰۤʤꡢ1 �����ʬ�Ǥϸ���������ϸ�����ؤ��Ѳ�����:
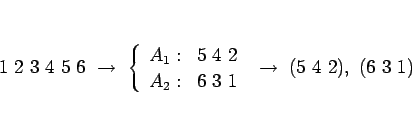
��äơ���ˡ A �ξ��˶�����ǽ�λ������ˤ� ��ˡ B �Ǥ����������Ǥ��� �����ǽ�λ������ˤϡ���ˡ B ��Ʊ�ͤΤ��Ȥ�Ԥʤ��� �߽�ˤʤäƤ��ޤ����Ȥˤʤ� (���Τˤ� B ��ǤϤ����ǤϤʤ������ʤ��Ȥ� A ��ǤϤ����ʤ�)�� ���ξ��ϡ��⤦ 1 ��Ĥλ��ˤ�����ʬ����� �����������ľ���뤳�Ȥˤʤ롣
��������ߤ�ȡ���ˡ B ��������ˡ A ������������ꤽ����
�����뤫�⤷��ʤ������ºݤˤϤ����ǤϤʤ���
�㤨�С����ٵս���¤� ![]() ,
,![]() ,...,3,2,1 ��ͤ���Ф狼�뤬��
�������ˡ A �ǤϺǰ��μ�����ɬ�פȤʤ뤬��
��ˡ B �ʤ� 1 �Ĥλ����ۤ������ 1 ��ǽ�λ���롣
�Ĥޤꡢ��ˡ B �ξ��ϡ�������֥��å��������Ǥʤ���
������֥��å��� �ˤ�äƤ��û��礬��ޤ뤳�Ȥˤʤ롣
,...,3,2,1 ��ͤ���Ф狼�뤬��
�������ˡ A �ǤϺǰ��μ�����ɬ�פȤʤ뤬��
��ˡ B �ʤ� 1 �Ĥλ����ۤ������ 1 ��ǽ�λ���롣
�Ĥޤꡢ��ˡ B �ξ��ϡ�������֥��å��������Ǥʤ���
������֥��å��� �ˤ�äƤ��û��礬��ޤ뤳�Ȥˤʤ롣
������֥��å����� ![]() ��������֥��å�����
��������֥��å����� ![]() �Ȥ���ȡ�
�����Ϥ��줾�츺���սꡢ���òս��� 1 �����礭����
�����սꡢ���òս�Ϥ������Ʊ�����ˤϤʤ���
��äƤ������¤�
�Ȥ���ȡ�
�����Ϥ��줾�츺���սꡢ���òս��� 1 �����礭����
�����սꡢ���òս�Ϥ������Ʊ�����ˤϤʤ���
��äƤ������¤� ![]() �Ǥ��뤫�顢
�Ǥ��뤫�顢
�ʤ���������֥��å����ϡ� A ����ž (�����ȿ�Фˤ�����) ��������֥��å������������� �ºݤκ�ȤǤ⡢�¤Ϥ��ε�ž���������������ǹͤ��뤳�Ȥˤʤ롣
�ưפˤ狼��褦�ˡ�������֥��å����ǹͤ������ϡ� ������֥��å��ǹͤ���ΤȤϵդǡ� ���줬��ˡ A �Ǵ����ǽ����֥��å����ʤ�С� ��ˡ B �Ǥ�Ʊ������Ǿ���ˤǤ��� ��ˡ A �Ƕ�����ǽ����֥��å����ʤ�С� ��ˡ B �Ǥ�Ʊ������ǤϹ߽�ˤʤäƤ��ޤ��Τ� �⤦ 1 ��ɬ�פȤʤ롣
��äơ����ξ��ϡ�
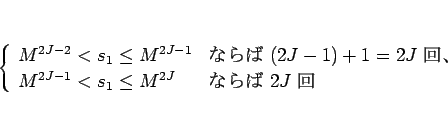
��ˡ B �ξ�硢
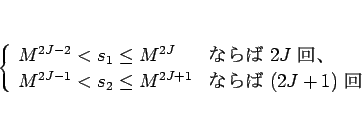
���줬��Ŭ�ʲ���Ǥ��뤳�Ȥ��ưפ˼�����롣![]() �Ǥ�����������롣
�㤨�С�A ��� 1,2,...,
�Ǥ�����������롣
�㤨�С�A ��� 1,2,...,![]() �ϡ���ˡ B �� 1 ������Ǥ�
�⡹ 2 �Ĥθ�����֥��å�����ʤ롣
��äơ�3 �İʾ�θ�����֥��å���ޤ� A ��κǽ����ϡ�
��ˡ B 1 ��Ǥϸ��ˤ��᤻�ʤ���
�ϡ���ˡ B �� 1 ������Ǥ�
�⡹ 2 �Ĥθ�����֥��å�����ʤ롣
��äơ�3 �İʾ�θ�����֥��å���ޤ� A ��κǽ����ϡ�
��ˡ B 1 ��Ǥϸ��ˤ��᤻�ʤ���
2 ��ǤϹ⡹ 4 �Ĥ�������֥��å�����ʤ���ˤʤ�Τǡ� 5 �İʾ��������֥��å�����Ĥ�Τ���ˡ B 2 ��Ǥϸ��ˤ��᤻�ʤ��� ���Τ褦�˹ͤ���С�̿�� 6 ��ɾ���� ��Ŭ�Ǥ��뤳�Ȥ��狼�롣
��ˡ B �ξ�硢����ؤ����ˤ� ����Ǥ�̿�� 6 �β������ɬ��