次へ: 8 方法 B の場合
上へ: sort1
前へ: 6 最適解の構成
(PDF ファイル: sort1-2.pdf)
7 並べ直しの具体例
ここでは、いくつか並べ直しの具体例を紹介する。
例 4
元々の数の並び (B 列の初期配列) が
9,4,3,5,8,2,1,7,6
であるとし、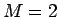 で考える。
で考える。
- まず A 列の最終形を求める。
- それを増加列ブロックに分割
(7), (6), (3), (2, 4, ,9), (8), (5), (1)
ブロック数は 7 個だから 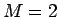 の場合は 3 回かかることになる。
の場合は 3 回かかることになる。
- ブロックの統合を行ない、昇順の初期配列に戻していく
ここで、(ア), (イ), (ウ) の [ ] 内の列は、
その上の行の A 列をどの山へ配分するかを意味する。
- この手順 (ア), (イ), (ウ) を B 列で逆にたどれば
B 列の整列化が行なえる
例 5
例 4 と同じ初期配列のものを 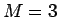 で整列化する。
この場合ブロック数は 7 個だから 2 回でできる。
で整列化する。
この場合ブロック数は 7 個だから 2 回でできる。
- A 列の最終形を求めて増加列ブロックに分割するところまでは
例 4 と同じ。
- ブロックの統合
- この手順 (ア), (イ) を B 列で逆にたどれば
B 列の整列化が行なえる
次へ: 8 方法 B の場合
上へ: sort1
前へ: 6 最適解の構成
竹野茂治@新潟工科大学
2006年2月24日
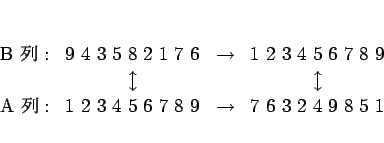
![\begin{eqnarray*}&& (7) (6) (3) (2 4 9) (8) (5) (1)
\leftarrow
\le...
...{]} & (ウ)
\end{tabular}}
\hspace{1zw}(\mbox{A 列の初期状態})
\end{eqnarray*}](img67.gif)

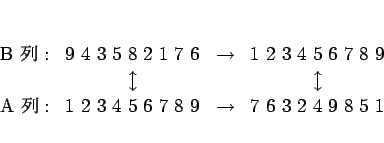
![\begin{eqnarray*}&& (7) (6) (3) (2 4 9) (8) (5) (1)
\leftarrow
\le...
...{]} & (ウ)
\end{tabular}}
\hspace{1zw}(\mbox{A 列の初期状態})
\end{eqnarray*}](img67.gif)

![]() で整列化する。
この場合ブロック数は 7 個だから 2 回でできる。
で整列化する。
この場合ブロック数は 7 個だから 2 回でできる。
![\begin{eqnarray*}&& (7) (6) (3) (2 4 9) (8) (5) (1)
\leftarrow
\le...
...{]} & (イ)
\end{tabular}}
\hspace{1zw}(\mbox{A 列の初期状態})
\end{eqnarray*}](img69.gif)
