5 オイラーの公式を用いた積の公式の証明
[2] では、
オイラーの公式を用いた考察もしているが、
その方法を用いれば (10), (11) は、
前節の方法よりはかなり易しく示すことができる。
本節ではその証明を紹介する。
そしてついでに (12), (13) も
同じ方法で証明するが、
多分 [2] で触れている (12) の
証明 (証明自体は書かれていない) も同様の方法を用いるのだろうと思う。
なお、この方法の場合は、前節で扱った (11) よりも
(10) の方が取り扱いは易しいので、こちらを考えることにする。
オイラーの公式を用いて 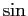 を指数関数で表せば、
を指数関数で表せば、
と変形できる。ここで、 の前の部分は、
の前の部分は、
であり、また  の部分は、
の部分は、
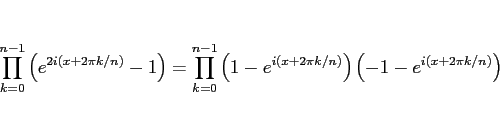 |
(19) |
と変形できるが、
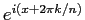 は、
は、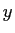 に関する
に関する 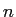 次方程式
次方程式
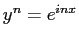 の
の 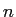 個の解であるから、代数学の基本定理により恒等式
個の解であるから、代数学の基本定理により恒等式
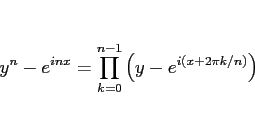 |
(20) |
が成り立つはずである。
これを用いれば、(19) は、(20) に 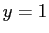 を
代入したものと
を
代入したものと 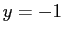 を代入したものの積なので、
これらを合わせると
を代入したものの積なので、
これらを合わせると 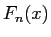 は
は
と書けることになる。ここで、
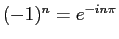 とすると、
とすると、
となることがわかる。
ここで、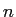 が奇数なら
が奇数なら
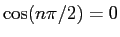 なので
なので
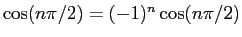 であるし、
また加法定理により、
であるし、
また加法定理により、
となるので、よって (21) は、
と書き直すことができ、これで (10) が示されたことになる。
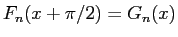 であるから、(11) は (10) に
であるから、(11) は (10) に 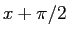 を代入すれば得られる。
を代入すれば得られる。
(12) は、(10) から得られなくもない
が (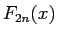 を用いればよい)、
ここでは
を用いればよい)、
ここでは 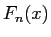 と同様の手法で直接示すことにする。
(12) の左辺を
と同様の手法で直接示すことにする。
(12) の左辺を 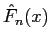 とすると、
とすると、
となるが、(20) の 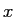 を
を 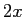 としたものに
としたものに 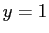 を代入すれば、
を代入すれば、
となり、(12) が得られる。
さらにこの式で 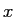 を
を 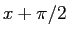 とすれば (13) が
得られる。
とすれば (13) が
得られる。
竹野茂治@新潟工科大学
2017年12月8日
![]() を指数関数で表せば、
を指数関数で表せば、
![]() が奇数なら
が奇数なら
![]() なので
なので
![]() であるし、
また加法定理により、
であるし、
また加法定理により、
![]() であるから、(11) は (10) に
であるから、(11) は (10) に ![]() を代入すれば得られる。
を代入すれば得られる。
![]() を用いればよい)、
ここでは
を用いればよい)、
ここでは ![]() と同様の手法で直接示すことにする。
(12) の左辺を
と同様の手法で直接示すことにする。
(12) の左辺を ![]() とすると、
とすると、