2 簡単な値になること
私は知らなかったが、
ネットで検索してみるとこの問題は割と有名なようで、
質問サイト等にかなりあがっているし、
Wikipedia [1] や、冨田 [2] などでも
説明されている。
それらに 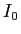 が簡単な値になる計算も書かれているが、
それをまず紹介する。使うのは積和の公式:
が簡単な値になる計算も書かれているが、
それをまず紹介する。使うのは積和の公式:
と、その逆の和積の公式である。
まず、(2), (3) により
となり、
となる。よって、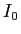 が簡単な値となるためには、
この後半の
が簡単な値となるためには、
この後半の
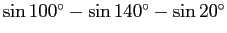 が
簡単な値となる必要があるが、これらを
が
簡単な値となる必要があるが、これらを 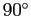 以下の角に直すと
以下の角に直すと
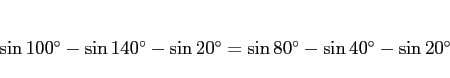 |
(4) |
となって、また 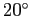 ,
, 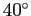 ,
, 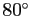 の角がでてくる。
これに今度は和積の公式を用いると、
の角がでてくる。
これに今度は和積の公式を用いると、
となるので、確かに (4) が 0 となり、よって
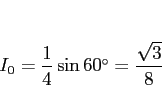 |
(6) |
が得られる。
上の流れを見ると、
三角比の値が容易には求まらない 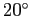 ,
, 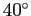 ,
, 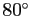 という角で
簡単な値の (6) が得られるのは、
その前の (5) で
という角で
簡単な値の (6) が得られるのは、
その前の (5) で
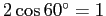 によって (4) の値が 0 となることがうまく働いているように見える。
によって (4) の値が 0 となることがうまく働いているように見える。
この話を一般化するため、
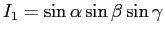 (
(
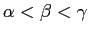 ) に積和の公式を用いて
) に積和の公式を用いて
と変形し、前の計算と比較することで、
の形であれば、
となることに気がついたので、とりあえず、
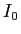 が (6) となるのは、
が (6) となるのは、
という構造があるようです、と答えておいた。
しかし、(4) の値が 0 になることが少し気になったので、
あらためて考えてみると、
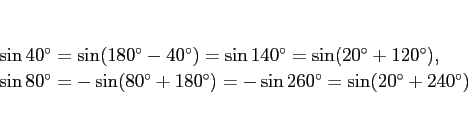 |
(7) |
と書き直すことができるので、よって (4) は、
の形になるが、これはよく知られた
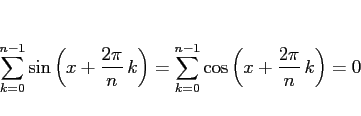 |
(8) |
の特別な場合であり、そのあたりに関連するとわかる。
特に、(7) の関係から、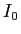 も
も
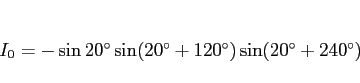 |
(9) |
となるので、そのあたりに一般的な性質が成り立つのでは、
と思い、手元の公式集 [3], [4] を見てみると
やはり以下のものがあった。
さらに、今回検索で見つけた、本稿に似た考察を行っている [2] では
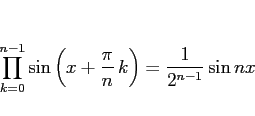 |
(12) |
についても触れているが、これも公式集 [3], [4] の
いずれにも書かれている。
なお、この (12) の 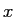 に
に 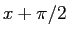 を代入すれば、
もちろん
を代入すれば、
もちろん
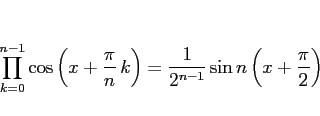 |
(13) |
も得られる。
これらを用いれば、(1) のような、
一見求まらなそうな角に対する三角関数の積がきれいな数字になる例は
かなり作れそうであることがわかる。
また、元の問題のように、(9) ではなく、
一見対称性がなさそうな (1) の形にしておけば
不思議さもより増すことだろう。
なお、冨田 [2] では、(9) のような等差系の
角の話だけではなく、(1) の形の 2 倍の等比系の
角についても言及している。
竹野茂治@新潟工科大学
2017年12月8日
![]() が簡単な値になる計算も書かれているが、
それをまず紹介する。使うのは積和の公式:
が簡単な値になる計算も書かれているが、
それをまず紹介する。使うのは積和の公式:
![]() ,
, ![]() ,
, ![]() という角で
簡単な値の (6) が得られるのは、
その前の (5) で
という角で
簡単な値の (6) が得られるのは、
その前の (5) で
![]() によって (4) の値が 0 となることがうまく働いているように見える。
によって (4) の値が 0 となることがうまく働いているように見える。
![]() (
(
![]() ) に積和の公式を用いて
) に積和の公式を用いて