6 最後に
本稿では、(1) に関連して、
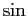 ,
, 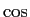 の
の 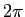 の等分角に対する和や積に関する公式などを
紹介した。これらが一応元の質問に対する回答になるかと思う。
の等分角に対する和や積に関する公式などを
紹介した。これらが一応元の質問に対する回答になるかと思う。
なお、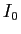 と似ているが、
と似ているが、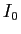 を
を 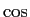 に変えた
に変えた
の方は、倍角の公式の繰り返しによって容易に、
と変形できるので、元の質問者はこれと似た方法、
あるいは同程度の易しい回答を期待していたかもしれないが、
そうだとすると、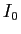 はそれとはだいぶ構造は違うため、
かなり難しい話になってしまったので、
これは期待通りでの回答ではなかったかもしれない。
はそれとはだいぶ構造は違うため、
かなり難しい話になってしまったので、
これは期待通りでの回答ではなかったかもしれない。
ただ、この問題に関連して、私も色々な公式を見ることができたし、
質問者にも元の問題の背景にある一般的な数学的構造が
多少でも見えてくれれば、それでよいのではないかと思う。
さらに、これらが何かの参考になれば幸いである。
竹野茂治@新潟工科大学
2017年12月8日
![]() と似ているが、
と似ているが、![]() を
を ![]() に変えた
に変えた