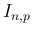 の最終形 (31 ) は、
の最終形 (31 ) は、
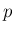 が整数の場合よりも実数の場合の方がむしろシンプルな形になったが、
そういったことは数学ではそれほど珍しいことではなく、
が整数の場合よりも実数の場合の方がむしろシンプルな形になったが、
そういったことは数学ではそれほど珍しいことではなく、
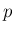 が整数の場合には丁度特異性が現れ実数の場合よりも
特殊な形になっているわけである。
そのような場合には、整数の場合だけを考えるよりも
実数に一般化した方がむしろ見通しが良くなる。
が整数の場合には丁度特異性が現れ実数の場合よりも
特殊な形になっているわけである。
そのような場合には、整数の場合だけを考えるよりも
実数に一般化した方がむしろ見通しが良くなる。
なお、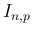 の最終形 (31 ) は、
の最終形 (31 ) は、
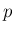 が整数の場合よりも実数の場合の方がむしろシンプルな形になったが、
そういったことは数学ではそれほど珍しいことではなく、
が整数の場合よりも実数の場合の方がむしろシンプルな形になったが、
そういったことは数学ではそれほど珍しいことではなく、
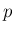 が整数の場合には丁度特異性が現れ実数の場合よりも
特殊な形になっているわけである。
そのような場合には、整数の場合だけを考えるよりも
実数に一般化した方がむしろ見通しが良くなる。
が整数の場合には丁度特異性が現れ実数の場合よりも
特殊な形になっているわけである。
そのような場合には、整数の場合だけを考えるよりも
実数に一般化した方がむしろ見通しが良くなる。
また、本稿で紹介したガンマ関数に関する公式 (25)
(相補公式、相反公式などとも呼ばれる) も、補題 1 と
同様の複素積分で証明ができるが、その前に広義 2 重積分や変数変換なども
必要とするので少し大掛かりである。
ただ、この相補公式の証明も色々あるようで、
例えば、[2], [3] には、
第 IV 章 15 定理 15.5 のガンマ関数の 1/2 公式などを用いる方法、
第 IX 章 9 例 4 の複素積分による方法、
例 9 のメリン変換の計算を行う方法、10 定理 10.8 の無限積展開を
利用する方法などの証明が紹介されている。
[5] にも第 5 章 5.12 例 5 の複素積分と 5.20 に
証明が紹介されているし、
ネット上にもいくつか証明が紹介されているようである。
左辺を 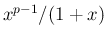 の広義積分に帰着させ、
の広義積分に帰着させ、
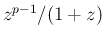 の複素積分を使う方法がシンプルであるが、
の複素積分を使う方法がシンプルであるが、
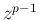 の分岐に注意する必要がある。
これも合わせて調べてみると勉強になると思う。
の分岐に注意する必要がある。
これも合わせて調べてみると勉強になると思う。
竹野茂治@新潟工科大学