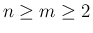 , または
, または 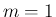 かつ
かつ 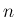 が奇数
のときに収束し、それ以外は発散することを示したが、
(2) の
が奇数
のときに収束し、それ以外は発散することを示したが、
(2) の 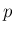 が実数の場合は、
まず
が実数の場合は、
まず
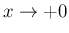 では
では
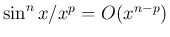 なので、
なので、
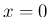 の近くでリーマン広義積分が収束するためには、
の近くでリーマン広義積分が収束するためには、
[1] では、
(1) は 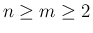 , または
, または 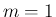 かつ
かつ 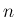 が奇数
のときに収束し、それ以外は発散することを示したが、
(2) の
が奇数
のときに収束し、それ以外は発散することを示したが、
(2) の 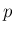 が実数の場合は、
まず
が実数の場合は、
まず
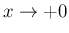 では
では
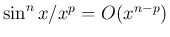 なので、
なので、
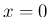 の近くでリーマン広義積分が収束するためには、
の近くでリーマン広義積分が収束するためには、
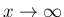 では、
では、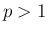 ならば (2) は
絶対可積分 (ルベーグ可積分) であるからリーマン広義積分としても収束し、
ならば (2) は
絶対可積分 (ルベーグ可積分) であるからリーマン広義積分としても収束し、
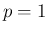 では
では 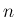 が奇数のときのみリーマン広義積分は収束していたが、
が奇数のときのみリーマン広義積分は収束していたが、
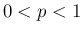 のときはさらに積分可能性 (収束性) が落ちることが予想されるが、
実は
のときはさらに積分可能性 (収束性) が落ちることが予想されるが、
実は 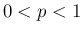 でもやはり
でもやはり 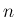 が奇数であれば
リーマン広義積分可能であることが言える。
その元になるのは次の補題である。
が奇数であれば
リーマン広義積分可能であることが言える。
その元になるのは次の補題である。
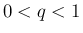 に対し、広義積分
に対し、広義積分
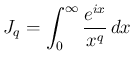
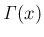 はガンマ関数
はガンマ関数
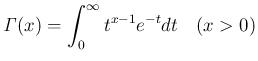
この補題は、
の両方の収束性を保証することになるが、[1] で見たように のときは
のときは
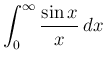
 の近くで収束しなかったからであり、
の近くで収束しなかったからであり、
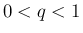 では (5) の前者は
では (5) の前者は  の近くでも
積分が収束するためにその有限性の可能性もあることに注意する。
の近くでも
積分が収束するためにその有限性の可能性もあることに注意する。
証明
複素積分を利用する。
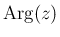 を
を ![$(-\pi,\pi]$](img28.png) での偏角の主値 (
での偏角の主値 (
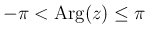 ) とし、
) とし、
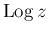 をそれに対する複素対数
をそれに対する複素対数 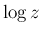 の主値
の主値
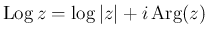
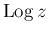 は複素数平面から実軸の負の部分を除いた領域で一価でかつ正則で、
これに対し、
は複素数平面から実軸の負の部分を除いた領域で一価でかつ正則で、
これに対し、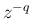 もその主値を取って、
とすれば、これも同じ領域で 1 価の正則関数となる。
もその主値を取って、
とすれば、これも同じ領域で 1 価の正則関数となる。
今、
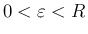 に対し、図 1 のように
領域
に対し、図 1 のように
領域 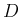 とその境界である積分路
とその境界である積分路
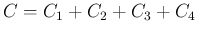 を取る。
を取る。
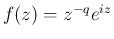 とすると、
とすると、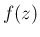 は
は 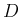 の内部で正則なので、
コーシーの積分定理により、
の内部で正則なので、
コーシーの積分定理により、
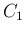 上の積分は、
となり、これは
上の積分は、
となり、これは
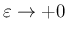 ,
,
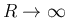 の
ときに
の
ときに 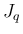 になる。
になる。
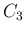 上の積分は、
上の積分は、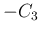 (
(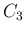 の逆向き) が
の逆向き) が 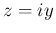 (
(
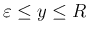 ) で表されるので、
) で表されるので、
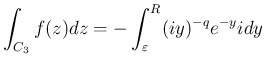
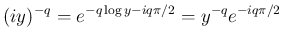
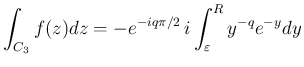
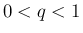 であれば
であれば
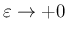 ,
,
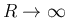 に対して収束し、
となることがわかる。
に対して収束し、
となることがわかる。
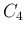 では、
では、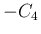 を
を
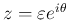
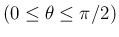 とすると、
とすると、
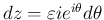 より
より
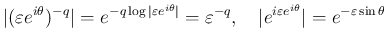
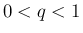 より
より
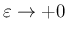 のときに
となることがわかる。
のときに
となることがわかる。
最後に 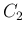 では
では
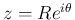 (
(
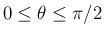 ) とすれば、
) とすれば、
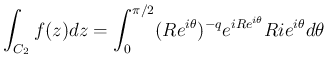
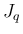 が収束して、
(4) が成り立つことがわかる。
よってあとは (15) を示せばよい。
が収束して、
(4) が成り立つことがわかる。
よってあとは (15) を示せばよい。
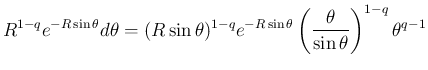
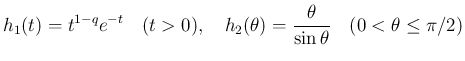
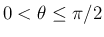 に対し、
に対し、
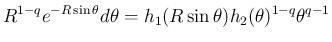
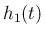 は、
は、
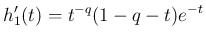
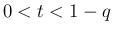 で
で 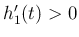 ,
, 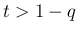 で
で 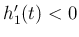 ,
,
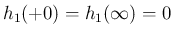 なので
なので 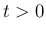 の最大値は
の最大値は 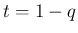 で取り、
よって、
で取り、
よって、
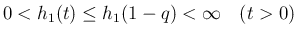
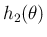 は
は
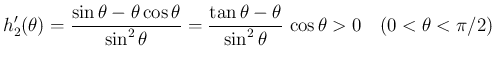
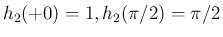 より、
より、
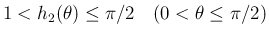
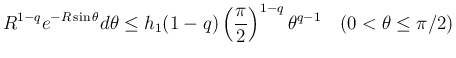
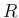 には無関係で、その積分は
には無関係で、その積分は
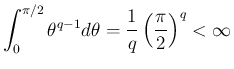
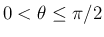 に対し、
に対し、
竹野茂治@新潟工科大学