4 連立漸化式
次に、連立の定数係数線形漸化式について考えてみる。
例えば、フィボナッチ数列の 2 つの解
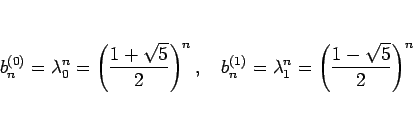
には、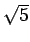 が含まれているが、
これらを展開すればいずれも有理数と
が含まれているが、
これらを展開すればいずれも有理数と 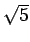 の有理数倍の和で書ける。
実際、二項定理により
の有理数倍の和で書ける。
実際、二項定理により
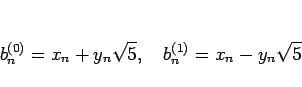 |
(13) |
(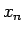 ,
, 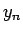 は有理数) の形になることが容易にわかる。
この
は有理数) の形になることが容易にわかる。
この 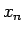 ,
, 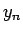 の満たす漸化式を考えてみよう。
の満たす漸化式を考えてみよう。
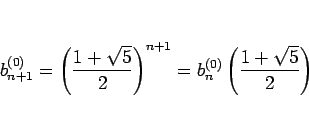
であるから、
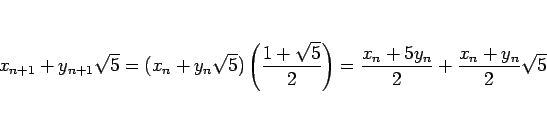
となる。よって、
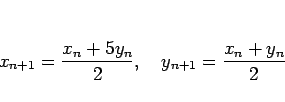 |
(14) |
となることがわかる。
これに 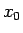 ,
, 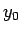 を与えることで、
順次
を与えることで、
順次 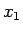 ,
, 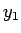 ,
, 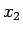 ,
, 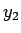 ,...と数列の値が決まっていくことになる。
,...と数列の値が決まっていくことになる。
一般に、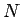 次元列ベクトルの列
次元列ベクトルの列
![\begin{displaymath}
X_n=\left[\begin{array}{c}x^{(0)}_n\\ x^{(1)}_n\\ \vdots\\ x^{(N-1)}_n\end{array}\right]\hspace{1zw}(n=0,1,2,\ldots)
\end{displaymath}](img125.gif)
と、成分が定数である 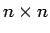 行列
行列 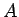 に対して、
に対して、
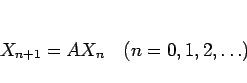 |
(15) |
を 定数係数連立線形同次漸化式 と呼ぶ。(14) は、
![\begin{displaymath}
A=\left[\begin{array}{cc}1/2 & 5/2\\ 1/2 & 1/2\end{array}\r...
...ace{1zw}
X_n=\left[\begin{array}{c}x_n\\ y_n\end{array}\right]\end{displaymath}](img129.gif) |
(16) |
の場合になっている。
(15) より、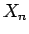 は、
は、
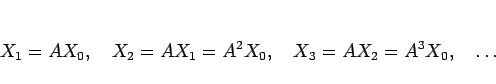
のようになるから、一般に
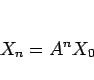 |
(17) |
と書けることがわかる。
よって、
この行列の 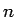 乗の
乗の 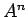 を行列の対角化などを使って求めれば、
(17) によって一般項
を行列の対角化などを使って求めれば、
(17) によって一般項 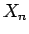 が求まることになるが、
それは少し難しい。
一方で、(15) を 2, 3 節で
考察した単独の (連立でない) 線形同次漸化式に帰着させる方法もある。
ここではそちらの方を説明する。
が求まることになるが、
それは少し難しい。
一方で、(15) を 2, 3 節で
考察した単独の (連立でない) 線形同次漸化式に帰着させる方法もある。
ここではそちらの方を説明する。
行列 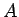 の固有方程式を
の固有方程式を
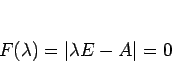
とすると、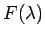 は
は 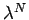 の係数が 1 の
の係数が 1 の 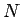 次式になる。
この
次式になる。
この 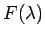 を
を
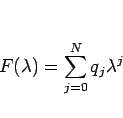 |
(18) |
と書く (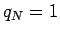 ) と、良く知られているようにケーリー・ハミルトンの関係式
) と、良く知られているようにケーリー・ハミルトンの関係式
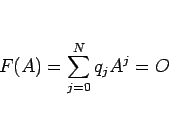 |
(19) |
(ただし、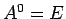 ) が成り立つ。
この両辺を右から
) が成り立つ。
この両辺を右から 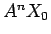 倍すると
倍すると
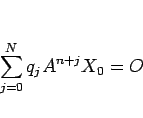
となるが、(17) よりこれは
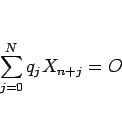
と書ける。そしてこれは、
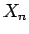 の成分
の成分 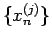 すべてが、同じ線形同次漸化式
すべてが、同じ線形同次漸化式
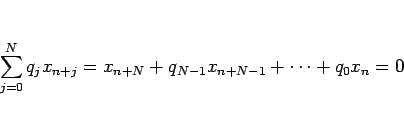 |
(20) |
を満たすことを意味している。
なお、この 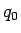 は、
は、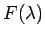 の定数項であるから、
の定数項であるから、
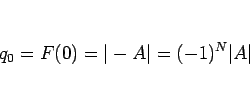
となっている。
よってこれが条件 (4) を満たすことは 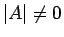 、
すなわち
、
すなわち 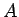 が正則であることと同値となる。
以下、
が正則であることと同値となる。
以下、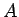 は正則であるとして考える。
は正則であるとして考える。
この場合は、3 節で見たように特性方程式により解が求まる。
(20) の特性方程式は、
(18) より固有方程式 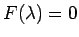 自体であるから、
つまり
自体であるから、
つまり 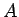 の固有方程式の解である固有値によって (20) の解が求まることになる。
の固有方程式の解である固有値によって (20) の解が求まることになる。
それによる (20) の 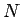 個の一次独立な解を
個の一次独立な解を
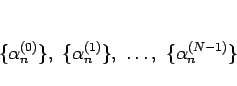
とし、
![\begin{displaymath}
Y_n=\left[\begin{array}{c}\alpha^{(0)}_n\\ \alpha^{(1)}_n\\ \vdots\\ \alpha^{(N-1)}_n\end{array}\right]
\end{displaymath}](img152.gif)
とすると、次が言える。
補題 3
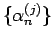 (
(
 ) が一次独立なら
) が一次独立なら  次元列ベクトル
次元列ベクトル 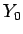 ,
, 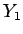 , ...
, ...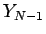 も一次独立。
も一次独立。
証明
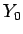 ,
, 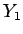 , ...
, ...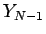 が一次独立でないとすれば、
が一次独立でないとすれば、
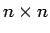 行列
行列
![\begin{displaymath}[Y_0\ Y_1\ \cdots\ Y_{N-1}]
\end{displaymath}](img157.gif)
の行列式の値は 0 となる。よって、この行列の行ベクトル
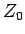 ,
, 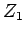 , ...,
, ..., 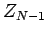 も一次独立ではないことになる。
ここで、
も一次独立ではないことになる。
ここで、
![\begin{displaymath}
Z_j=[\alpha^{(j)}_0\ \alpha^{(j)}_1\ \cdots \ \alpha^{(j)}_{N-1}]
\end{displaymath}](img161.gif)
であるから、これらが一次従属ならば、
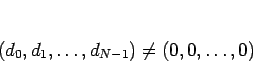 |
(21) |
である定数 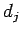 に対して、
に対して、
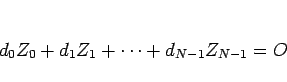
と書けることになる。成分で見ればこれは、
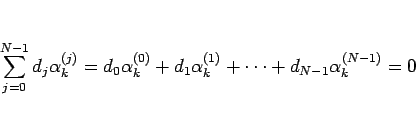 |
(22) |
が
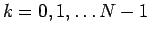 に対して成り立つことを意味する。
(20) を考えれば、この (22) は
に対して成り立つことを意味する。
(20) を考えれば、この (22) は 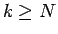 に対しても成り立つことになる。
例えば
に対しても成り立つことになる。
例えば 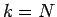 に対しては、
に対しては、
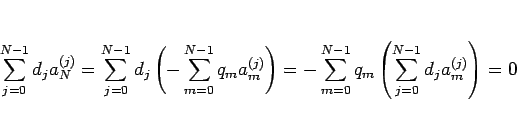
が (22) から言える。以下同様である。
そして (21) と (22) は、
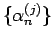 (
(
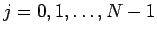 ) が一次従属であることを意味する。
) が一次従属であることを意味する。
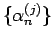 (
(
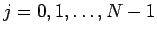 ) は、
(20) の
) は、
(20) の 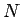 個の一次独立な解であるから、
命題 1 によって
個の一次独立な解であるから、
命題 1 によって 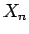 の成分
の成分 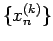 はそれらの
一次結合で表される。よって、
はそれらの
一次結合で表される。よって、
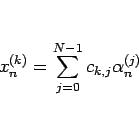
のようになるので、
これにより 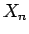 はこの係数による行列
はこの係数による行列 ![$C=[c_{k,j}]$](img171.gif) と
と 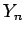 により
により
![\begin{displaymath}
X_n=CY_n\hspace{1zw}(C=[c_{k,j}])\end{displaymath}](img173.gif) |
(23) |
と書けることになる。後は、この係数行列 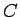 を初期値から決めればよい。
すなわち、
を初期値から決めればよい。
すなわち、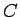 を
を 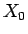 と
と 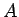 を用いて表せばよいことになる。
(23) の
を用いて表せばよいことになる。
(23) の
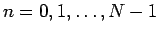 の式を行列にまとめて書けば、
の式を行列にまとめて書けば、
![\begin{displaymath}[X_0\ X_1\ \cdots\ X_{N-1}]=C[Y_0\ Y_1\ \cdots\ Y_{N-1}]
\end{displaymath}](img177.gif)
となるが、補題 3 より
行列
![$[Y_0\ Y_1\ \cdots\ Y_{N-1}]$](img178.gif) は正則であり、
また (17) を用いて左辺を書き直せば、結局
は正則であり、
また (17) を用いて左辺を書き直せば、結局 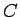 は
は
![\begin{displaymath}
C=[X_0\ AX_0\ \cdots\ A^{N-1}X_0][Y_0\ Y_1\ \cdots\ Y_{N-1}]^{-1}\end{displaymath}](img179.gif) |
(24) |
と書けることになる。
この (23) と (24) により、
行列 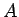 の
の 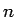 乗の計算をせずに連立漸化式の解が求められることになる。
乗の計算をせずに連立漸化式の解が求められることになる。
例として、今の方法を (14) に適用してみる。
初期値は、題意より 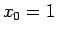 ,
, 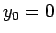 とする。
この場合、
とする。
この場合、 は (16) より、固有方程式は
は (16) より、固有方程式は
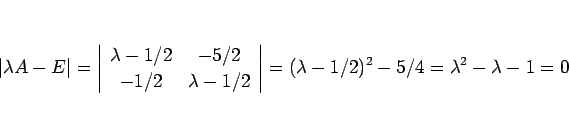
となって、結局フィボナッチ数列の特性方程式と同じになる。
よって、一次独立な二つの解は
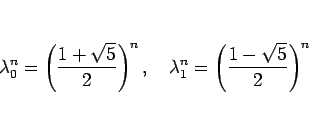
であり、よって
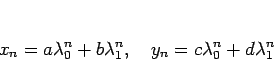
つまり、
![\begin{displaymath}
\left[\begin{array}{c}x_n\\ y_n\end{array}\right]=\left[\beg...
...ft[\begin{array}{c}\lambda_0^n\\ \lambda_1^n\end{array}\right]
\end{displaymath}](img185.gif)
と書ける。この係数行列を求めるには、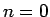 ,
, 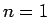 を考えれば、
を考えれば、
![\begin{displaymath}
\left[\begin{array}{c}x_0\\ y_0\end{array}\right]=\left[\beg...
...rray}\right]=\left[\begin{array}{c}1/2\\ 1/2\end{array}\right]
\end{displaymath}](img188.gif)
より、
![\begin{displaymath}
\left[\begin{array}{cc}1&1/2\\ 0&1/2\end{array}\right]
=\lef...
...t[\begin{array}{cc}1&\lambda_0\\ 1&\lambda_1\end{array}\right]
\end{displaymath}](img189.gif)
となるので、
![\begin{eqnarray*}\left[\begin{array}{cc}a&b\\ c&d\end{array}\right]
&=&
\left...
...\left[\begin{array}{cc}\sqrt{5}&\sqrt{5}\\ 1&-1\end{array}\right]\end{eqnarray*}](img190.gif)
より、結局、
![\begin{displaymath}
\left[\begin{array}{c}x_n\\ y_n\end{array}\right]
=
\frac{1}...
...le \frac{\lambda_0^n-\lambda_1^n}{2\sqrt{5}}\end{array}\right]
\end{displaymath}](img191.gif)
となる。
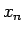 は、
は、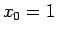 ,
, 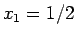 に対するフィボナッチ数列の解、
に対するフィボナッチ数列の解、
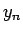 は
は 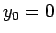 ,
, 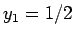 に対するフィボナッチ数列の解となっていて、
これらは 2 節の最後の
に対するフィボナッチ数列の解となっていて、
これらは 2 節の最後の 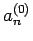 ,
, 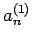 を用いれば、
を用いれば、
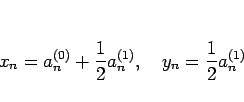
と書けることもわかる。
なお、この最後の 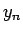 と
と 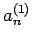 (
(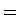 元々のフィボナッチ数列
元々のフィボナッチ数列 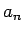 ) との関係は、(13) からもわかる。すなわち、
(2) および (13) より、
) との関係は、(13) からもわかる。すなわち、
(2) および (13) より、
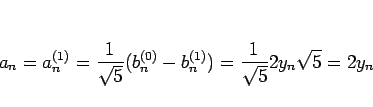
だからである。つまり、元のフィボナッチ数列の値は、
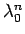 の
の 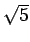 の係数である有理数の 2 倍であることになる。
の係数である有理数の 2 倍であることになる。
さらに、(9) より、
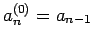 であるから、
であるから、
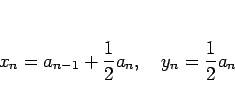
となり、そして
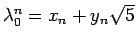 は
フィボナッチ数列
は
フィボナッチ数列 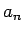 を用いて
を用いて
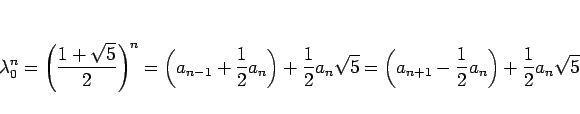
と書けることになる。
竹野茂治@新潟工科大学
2009年8月5日
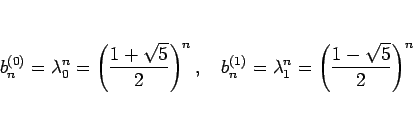
![]() 次元列ベクトルの列
次元列ベクトルの列
![]() は、
は、
![]() の固有方程式を
の固有方程式を
![]() は、
は、![]() の定数項であるから、
の定数項であるから、
![]() 自体であるから、
つまり
自体であるから、
つまり ![]() の固有方程式の解である固有値によって (20) の解が求まることになる。
の固有方程式の解である固有値によって (20) の解が求まることになる。
![]() 個の一次独立な解を
個の一次独立な解を
![]() (
(
![]() ) が一次独立なら
) が一次独立なら ![]() 次元列ベクトル
次元列ベクトル ![]() ,
, ![]() , ...
, ...![]() も一次独立。
も一次独立。
![]() ,
, ![]() , ...
, ...![]() が一次独立でないとすれば、
が一次独立でないとすれば、
![]() 行列
行列
![]() (
(
![]() ) は、
(20) の
) は、
(20) の ![]() 個の一次独立な解であるから、
命題 1 によって
個の一次独立な解であるから、
命題 1 によって ![]() の成分
の成分 ![]() はそれらの
一次結合で表される。よって、
はそれらの
一次結合で表される。よって、
![]() ,
, ![]() とする。
この場合、
とする。
この場合、![]() は (16) より、固有方程式は
は (16) より、固有方程式は
![]() は、
は、![]() ,
, ![]() に対するフィボナッチ数列の解、
に対するフィボナッチ数列の解、
![]() は
は ![]() ,
, ![]() に対するフィボナッチ数列の解となっていて、
これらは 2 節の最後の
に対するフィボナッチ数列の解となっていて、
これらは 2 節の最後の ![]() ,
, ![]() を用いれば、
を用いれば、
![]() と
と ![]() (
(![]() 元々のフィボナッチ数列
元々のフィボナッチ数列 ![]() ) との関係は、(13) からもわかる。すなわち、
(2) および (13) より、
) との関係は、(13) からもわかる。すなわち、
(2) および (13) より、
![]() であるから、
であるから、