3 解の構造
2 節の命題 1 により、
(3) の解を求めるには 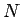 個の線形独立な解を求めればよいことがわかったが、
それはいわゆる特性方程式によって求めることができる。
個の線形独立な解を求めればよいことがわかったが、
それはいわゆる特性方程式によって求めることができる。
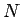 次方程式
次方程式
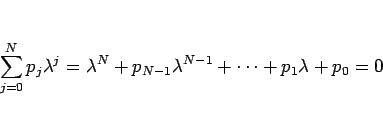 |
(10) |
を、(3) の 特性方程式 と呼ぶ。
これは一般には 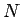 個の複素数解を持つが、
条件 (4) によりそれらはいずれも 0 ではない。
個の複素数解を持つが、
条件 (4) によりそれらはいずれも 0 ではない。
(10) を 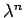 倍すると、
倍すると、
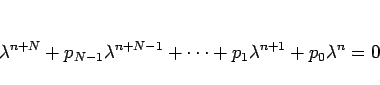
となる。
これはすなわち 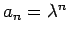 が (3) の
解の一つであることを意味している1。
が (3) の
解の一つであることを意味している1。
よって、特性方程式 (10) の解
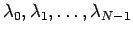 がすべて違っていれば、
がすべて違っていれば、
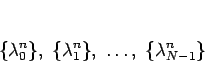
が一次独立であることは、例えばファンデルモンドの行列式によってわかるから、
(3) の一般解は、
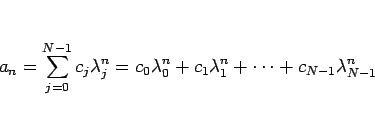
と表されることになる。
問題は特性方程式 (10) が重解を持つ場合であるが、
この場合は次が成り立つ。
命題 2
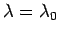 が (10) の
が (10) の 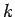 重解の場合 (
重解の場合 (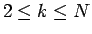 )、
)、
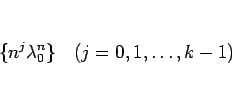
の 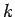 個の一次独立な数列がすべて (3) の解となる。
個の一次独立な数列がすべて (3) の解となる。
証明
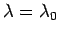 が (10) の
が (10) の 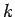 重解であれば、
(10) の左辺は
重解であれば、
(10) の左辺は
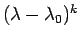 を因数に持つので、
(10) の左辺を
を因数に持つので、
(10) の左辺を 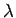 で微分した式に
で微分した式に
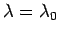 を
代入すれば 0 となる。
よって、
を
代入すれば 0 となる。
よって、
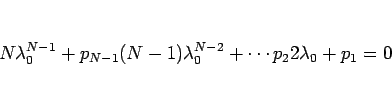
が成り立つ。
この式を 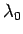 倍すると
倍すると
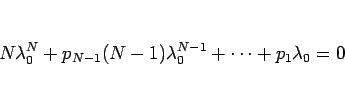 |
(11) |
となるが、これに、
(10) に
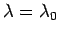 を代入して
を代入して 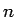 倍したものを加えると、
倍したものを加えると、
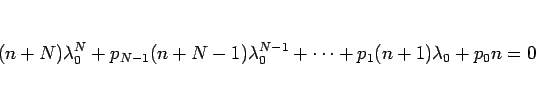
となるが、これをさらに 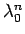 倍すれば
倍すれば
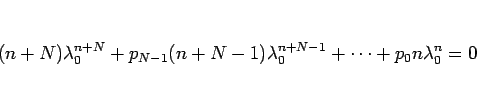
となる。
これは
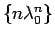 が (3) の解であることを
意味する。
が (3) の解であることを
意味する。
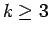 の場合は、(11) の左辺の
の場合は、(11) の左辺の 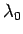 を
を 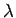 で置き換えた式
で置き換えた式
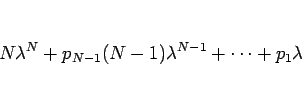
は、(10) の左辺を 1 回微分して 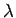 倍した式であるから、
倍した式であるから、
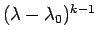 を因数に持つ。
よって、やはりこの式を微分したものに
を因数に持つ。
よって、やはりこの式を微分したものに
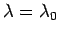 を
代入すれば 0 となる。
を
代入すれば 0 となる。
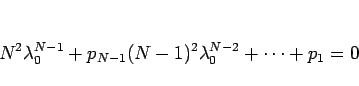
これを 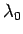 倍して、
倍して、
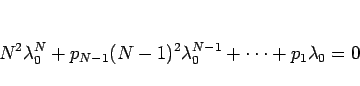
とし、
これに (11) の 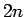 倍と、
(10) に
倍と、
(10) に 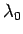 を代入して
を代入して 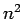 倍したものを加えると、
倍したものを加えると、
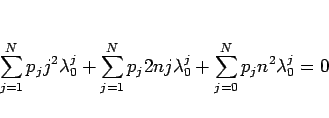
より
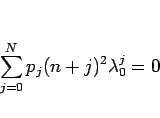
となるので、これを 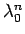 倍すれば、
倍すれば、
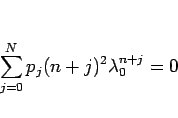
となる。
これは、
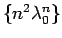 が (3) の解であることを
意味する。
が (3) の解であることを
意味する。
以下、これを繰り返せばよい。
これにより、(10) が重解を持つ場合も含めて (3) の解の構造がわかったことになる。
基本的には、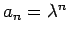 のように等比数列だと考えて得られるのが
特性方程式 (10) なので、
(3) の解がその形の解によってほぼ表現される、
というところが (3) の解の構造の本質となる。
のように等比数列だと考えて得られるのが
特性方程式 (10) なので、
(3) の解がその形の解によってほぼ表現される、
というところが (3) の解の構造の本質となる。
例えば、4 項漸化式
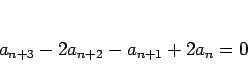
の場合、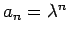 とすると
とすると
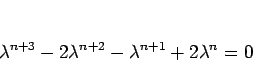
となるので、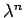 で割ると
で割ると
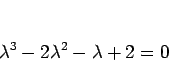
という 3 次方程式が得られるが、これが特性方程式である。これは、
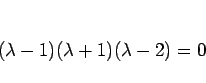
と因数分解されるので、
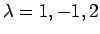 と求まる。よって、
と求まる。よって、
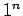 ,
, 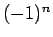 ,
, 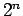 という一次独立な解があるので、一般解は、
という一次独立な解があるので、一般解は、
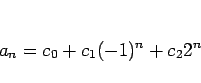
と表される。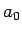 ,
, 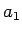 ,
, 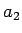 を与えれば、
それにより
を与えれば、
それにより 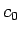 ,
, 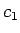 ,
, 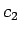 が決定され、一つの解が決まることになる。
が決定され、一つの解が決まることになる。
同様に、
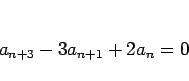
の場合は、特性方程式は
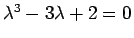 であり、これは
であり、これは
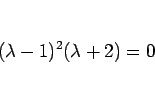
と因数分解され、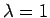 は重解になるので、
この場合の一次独立な解は命題 2 により
は重解になるので、
この場合の一次独立な解は命題 2 により
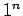 ,
, 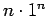 ,
, 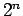 となり、よって、一般解は
となり、よって、一般解は
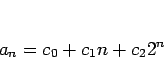
となる。
フィボナッチ数列
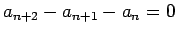 の場合は、特性方程式は
の場合は、特性方程式は
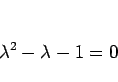 |
(12) |
であり、この解は
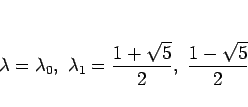
となる。よって、
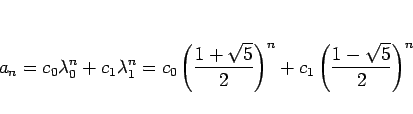
と表される。(1) の 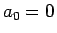 ,
, 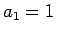 となる解を求めると、
となる解を求めると、
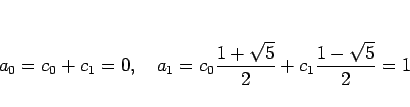
の連立方程式を解いて、
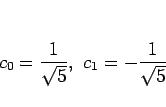
となり、これにより (2) が得られる。
つまり、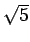 は、2 次方程式 (12) の解として
出てくるのであって、それを満たす
は、2 次方程式 (12) の解として
出てくるのであって、それを満たす 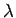 が
が
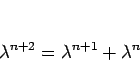
を満たすことで 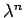 がフィボナッチ数列の解となるという
構造から (2) のような式が出てくるわけである。
このように、線形同次漸化式の解は、
基本的には (ほぼ) 等比数列の一次結合という構造になっている。
がフィボナッチ数列の解となるという
構造から (2) のような式が出てくるわけである。
このように、線形同次漸化式の解は、
基本的には (ほぼ) 等比数列の一次結合という構造になっている。
竹野茂治@新潟工科大学
2009年8月5日
![]() 次方程式
次方程式
![]() 倍すると、
倍すると、
![]() がすべて違っていれば、
がすべて違っていれば、
![]() が (10) の
が (10) の ![]() 重解の場合 (
重解の場合 (![]() )、
)、
![]() が (10) の
が (10) の ![]() 重解であれば、
(10) の左辺は
重解であれば、
(10) の左辺は
![]() を因数に持つので、
(10) の左辺を
を因数に持つので、
(10) の左辺を ![]() で微分した式に
で微分した式に
![]() を
代入すれば 0 となる。
よって、
を
代入すれば 0 となる。
よって、
![]() の場合は、(11) の左辺の
の場合は、(11) の左辺の ![]() を
を ![]() で置き換えた式
で置き換えた式
![]() のように等比数列だと考えて得られるのが
特性方程式 (10) なので、
(3) の解がその形の解によってほぼ表現される、
というところが (3) の解の構造の本質となる。
のように等比数列だと考えて得られるのが
特性方程式 (10) なので、
(3) の解がその形の解によってほぼ表現される、
というところが (3) の解の構造の本質となる。
![]() の場合は、特性方程式は
の場合は、特性方程式は
![]() は、2 次方程式 (12) の解として
出てくるのであって、それを満たす
は、2 次方程式 (12) の解として
出てくるのであって、それを満たす ![]() が
が