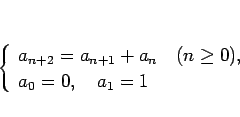1 はじめに
漸化式で決まる数列として代表的なものにフィボナッチ数列がある。
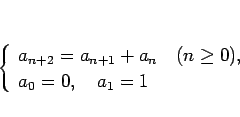 |
(1) |
これは、3 項の定数係数線形同次漸化式と分類されるものであるが、
この 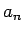 の一般項は次の形になることがよく知られている。
の一般項は次の形になることがよく知られている。
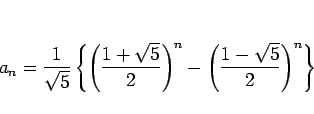 |
(2) |
(1) で得られる項はすべて整数であるのに、
一般項 (2) には 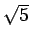 のような無理数が現れることに
不思議さを感じる人もいるようである。
のような無理数が現れることに
不思議さを感じる人もいるようである。
本稿では、一般の定数係数線形同次漸化式、
および連立の線形同次漸化式、非同次の漸化式の解 (一般項) の構造や
その求め方について考察を行うことで、
フィボナッチ数列の一般項の構造に関して考え直してみたいと思う。
なお、本稿ではある程度の線形代数の知識を仮定して話を進めることにする。
竹野茂治@新潟工科大学
2009年8月5日