2 定数係数線形同次漸化式
定数係数線形同次 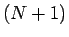 項漸化式とは、以下のような漸化式を言う。
項漸化式とは、以下のような漸化式を言う。
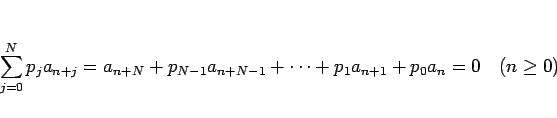 |
(3) |
ここで、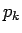 (
(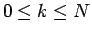 ) は定数で、
) は定数で、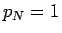 とする。
また、
とする。
また、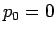 であれば、一つずらすことで
であれば、一つずらすことで 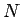 項以下の漸化式にできるので、
ここでは
項以下の漸化式にできるので、
ここでは
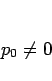 |
(4) |
であると仮定する。
まず、数列の線形性について述べておく。今、数列
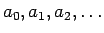 を
を
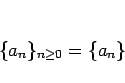
のように書くことにする。このとき、
2 つの数列 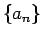 ,
, 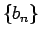 の和を
の和を 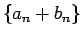 で定義でき、
また数列
で定義でき、
また数列 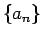 のスカラー倍 (
のスカラー倍 (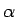 倍) を
倍) を
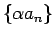 で
定義できる。これにより、数列
で
定義できる。これにより、数列 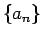 を抽象的なベクトルと見ることができ、
数列の集まりをベクトル空間 (線形空間) と考えることができる。
を抽象的なベクトルと見ることができ、
数列の集まりをベクトル空間 (線形空間) と考えることができる。
漸化式 (3) は、
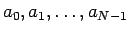 を与えれば
を与えれば
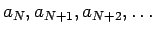 がこの漸化式によって順に求められていくから、
(3) を満たす数列には
がこの漸化式によって順に求められていくから、
(3) を満たす数列には 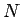 個の自由度があるといえる。
これを線形代数の言葉で表現すれば次の命題 1 のようになる。
なお、以下では (3) を満たす数列のことを (3) の 解 と呼ぶことにする。
個の自由度があるといえる。
これを線形代数の言葉で表現すれば次の命題 1 のようになる。
なお、以下では (3) を満たす数列のことを (3) の 解 と呼ぶことにする。
命題 1
-
(3) の解は、線形 (部分) 空間を作る
(これを (3) の 解空間 と呼ぶ)。
すなわち、(3) の解である 2 つの数列の和、
および (3) の解のスカラー倍も (3) の解となる。
- (3) の解空間の次元は丁度
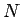 である。
すなわち、
である。
すなわち、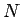 個の一次独立な数列
個の一次独立な数列 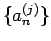 (
(
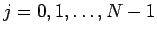 )
が存在して、解空間の任意の数列
)
が存在して、解空間の任意の数列 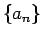 は、
ある定数
は、
ある定数 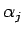 (
(
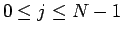 ) を用いて
) を用いて
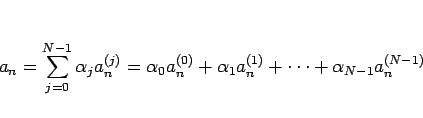
と書ける。
証明
1.
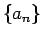 ,
, 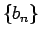 が (3) の解であれば、
が (3) の解であれば、
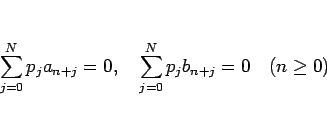
が成り立つから、任意のスカラー 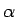 に対して、
に対して、
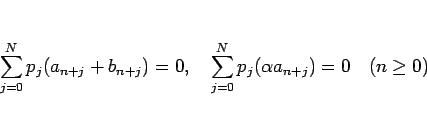
となるので、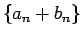 ,
,
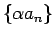 も (3) の解となる。よって、それらは線形空間を作る。
も (3) の解となる。よって、それらは線形空間を作る。
2.
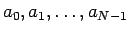 を与えれば (3) の解は
一意に決まるので、
を与えれば (3) の解は
一意に決まるので、
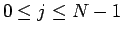 に対し、
に対し、
![\begin{displaymath}
\left[\begin{array}{c}a_0\\ a_1\\ \vdots\\ a_{N-1}\end{arra...
...\begin{array}{c}0\\ \vdots\\ 1\\ \vdots\\ 0\end{array}\right]
\end{displaymath}](img29.gif) |
(5) |
(
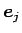 は上から
は上から 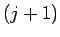 番目の成分が 1 で、
他の成分が全部 0 の
番目の成分が 1 で、
他の成分が全部 0 の 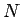 次元ベクトル) によって決まる (3) の解を
次元ベクトル) によって決まる (3) の解を 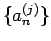 と書くことにすると、
これにより
と書くことにすると、
これにより 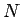 個の解が作られることになる。
この
個の解が作られることになる。
この 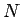 個の解は一次独立である。
実際、定数
個の解は一次独立である。
実際、定数 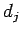 (
(
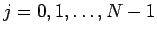 ) に対し、
) に対し、
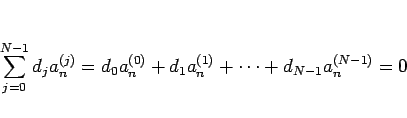 |
(6) |
がすべての 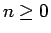 について成り立つとすると、
(5) により
について成り立つとすると、
(5) により 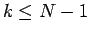 に対して
に対して
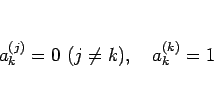 |
(7) |
が成り立つから、(6) で 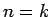 とすれば
とすれば 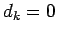 となる。
結局
となる。
結局 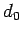 ,
, 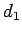 , ...はすべて 0 となるので、
よって
, ...はすべて 0 となるので、
よって 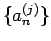 (
(
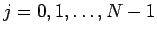 ) が一次独立であることがわかる。
) が一次独立であることがわかる。
また、(3) の任意の解 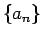 に対しても、
に対しても、
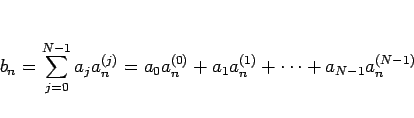 |
(8) |
とすると、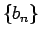 は
は 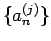 の一次結合であるから 1. により (3) の解の一つであり、
の一次結合であるから 1. により (3) の解の一つであり、
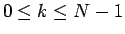 に対しては、
(7) より
に対しては、
(7) より 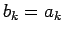 になっているので、
になっているので、
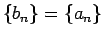 であることがわかる。
すなわち、任意の解
であることがわかる。
すなわち、任意の解 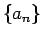 は (8) のように
は (8) のように
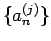 の一次結合として表されることになる。
の一次結合として表されることになる。
フィボナッチ数列 (1) で言えば、
(2) は 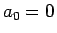 ,
, 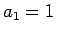 の解であるから、
これは命題 1 の 2. の
の解であるから、
これは命題 1 の 2. の 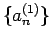 に当たる。もう一つの解である
に当たる。もう一つの解である 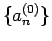 は、
は、
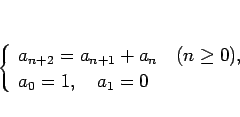
を満たすものとなるが、これは 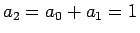 となるので、
となるので、
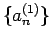 を一つずらしたものであることがわかる。すなわち、
を一つずらしたものであることがわかる。すなわち、
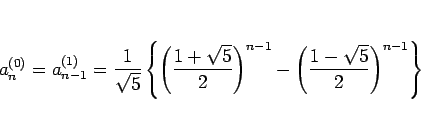 |
(9) |
となる。
竹野茂治@新潟工科大学
2009年8月5日
![]() を
を
![]() を与えれば
を与えれば
![]() がこの漸化式によって順に求められていくから、
(3) を満たす数列には
がこの漸化式によって順に求められていくから、
(3) を満たす数列には ![]() 個の自由度があるといえる。
これを線形代数の言葉で表現すれば次の命題 1 のようになる。
なお、以下では (3) を満たす数列のことを (3) の 解 と呼ぶことにする。
個の自由度があるといえる。
これを線形代数の言葉で表現すれば次の命題 1 のようになる。
なお、以下では (3) を満たす数列のことを (3) の 解 と呼ぶことにする。
![]() を与えれば (3) の解は
一意に決まるので、
を与えれば (3) の解は
一意に決まるので、
![]() に対し、
に対し、
![]() に対しても、
に対しても、
![]() ,
, ![]() の解であるから、
これは命題 1 の 2. の
の解であるから、
これは命題 1 の 2. の ![]() に当たる。もう一つの解である
に当たる。もう一つの解である ![]() は、
は、