4 N≧3 の場合
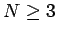 の場合の定理 1 の証明は、
3 節の
の場合の定理 1 の証明は、
3 節の 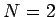 の場合の不等式 (5) を繰り返し用いることで示される (厳密には帰納法)。
の場合の不等式 (5) を繰り返し用いることで示される (厳密には帰納法)。
例えば 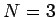 の場合を考えてみる。今、
の場合を考えてみる。今、
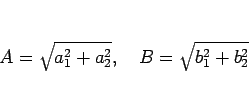
として、(5) の両辺に 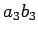 を加えると、
を加えると、
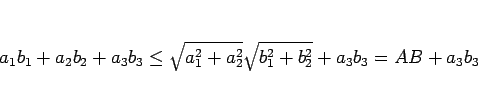 |
(10) |
となる。
この 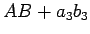 に、
に、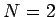 のシュワルツの不等式 (5) を適用すれば、
のシュワルツの不等式 (5) を適用すれば、
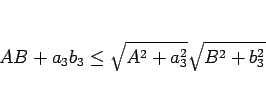 |
(11) |
となることがわかる。ここで、
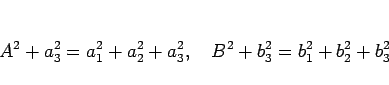
であるから、結局 (10), (11) により 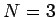 のシュワルツの不等式 (2) が示されたことになる。
のシュワルツの不等式 (2) が示されたことになる。
この等号成立条件は、(10), (11) の両方で等号が成立する場合であるから、
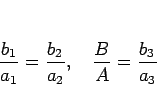
であることがわかる。
しかし、前者の等号成立の場合は (9) が成り立っていたので、結局
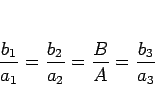
であることがわかり、
よって 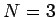 の (3) が言えたことになる。
そしてこの比は (9) により
の (3) が言えたことになる。
そしてこの比は (9) により
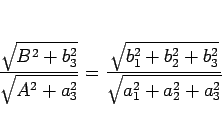
に等しいことも言える。
後はこれを繰り返していけば、
すべての自然数 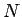 に対して定理 1 が成り立つことがわかる。
に対して定理 1 が成り立つことがわかる。
竹野茂治@新潟工科大学
2010年1月20日
![]() の場合を考えてみる。今、
の場合を考えてみる。今、
![]() に対して定理 1 が成り立つことがわかる。
に対して定理 1 が成り立つことがわかる。