3 N=2 の図形的な証明
本節では、定理 1 の 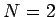 の場合に限って、
図形的な証明を試みる。
よってこの場合示すべきは、正の実数
の場合に限って、
図形的な証明を試みる。
よってこの場合示すべきは、正の実数
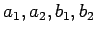 に対して
に対して
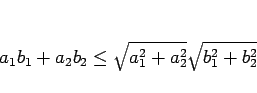 |
(5) |
が成り立つことと、この等号が成立するのが
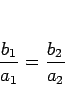 |
(6) |
のとき、ということになる。
まず、以下の 2 つの長方形 (図 1) を見比べて見てもらいたい。
この 2 つの長方形は、いずれも底辺 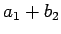 , 高さ
, 高さ 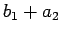 で、
4 つの直角三角形の配置を変えただけの同じ長方形なので、
で、
4 つの直角三角形の配置を変えただけの同じ長方形なので、
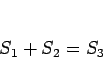 |
(7) |
であることがわかる。
この左辺は
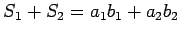 であるから (5) の左辺に等しく、
また
であるから (5) の左辺に等しく、
また 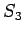 は平行四辺形で、その 2 辺は三平方の定理より
は平行四辺形で、その 2 辺は三平方の定理より
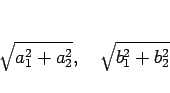
であることがわかる。
2 辺が決まった平行四辺形は、高さが最も高いときに面積は最大となるので、
よってその平行四辺形の面積は、その 2 辺が直角となった長方形の面積以下となる。
すなわち
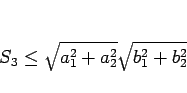 |
(8) |
となる。よって (7), (8) から (5) が成り立つことが示されたことになる。
次に、(5) の等号成立条件であるが、
これは (8) の等号が成り立つとき、
すなわち 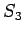 が長方形となるときを意味する (図 2)。
が長方形となるときを意味する (図 2)。
図 2:
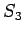 が長方形の場合
が長方形の場合
|
|
この場合は、図からわかるように、
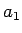 ,
, 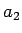 が直角を挟む直角三角形と
が直角を挟む直角三角形と 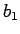 ,
, 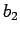 が直角を挟む直角三角形とが相似になるので、
よって (6) が成り立つことになる。
しかも、斜辺の比も考えれば、
が直角を挟む直角三角形とが相似になるので、
よって (6) が成り立つことになる。
しかも、斜辺の比も考えれば、
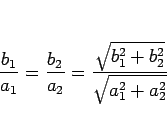 |
(9) |
となることもわかる。
竹野茂治@新潟工科大学
2010年1月20日
![]() , 高さ
, 高さ ![]() で、
4 つの直角三角形の配置を変えただけの同じ長方形なので、
で、
4 つの直角三角形の配置を変えただけの同じ長方形なので、
![]() が長方形となるときを意味する (図 2)。
が長方形となるときを意味する (図 2)。
![]() ,
, ![]() が直角を挟む直角三角形と
が直角を挟む直角三角形と ![]() ,
, ![]() が直角を挟む直角三角形とが相似になるので、
よって (6) が成り立つことになる。
しかも、斜辺の比も考えれば、
が直角を挟む直角三角形とが相似になるので、
よって (6) が成り立つことになる。
しかも、斜辺の比も考えれば、