2 相関係数とシュワルツの不等式
その方の言うには、相関係数 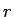 は、
は、
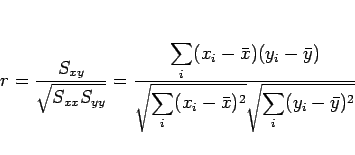 |
(1) |
であり、
分子は 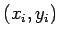 というデータ点と
というデータ点と
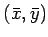 を 2 頂点とする長方形の面積の和だけど、
分母がよくわからない、
を 2 頂点とする長方形の面積の和だけど、
分母がよくわからない、
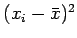 は
は 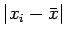 を一辺とする正方形の面積だから、
その正方形の面積を全部足したものを面積とするような正方形の一辺の長さが
を一辺とする正方形の面積だから、
その正方形の面積を全部足したものを面積とするような正方形の一辺の長さが
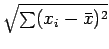 なんだろうけど、
それと
なんだろうけど、
それと 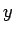 に対する同じようなものをかけたものは一体どういう意味か、
という話であった。
に対する同じようなものをかけたものは一体どういう意味か、
という話であった。
確かに上記の話自体に誤りはないし、
相関係数をイメージするために
数式を図形的にとらえようと考える工夫も論理的で非常に面白い。
ただ、それで分母に意味付けがなされて、
相関係数を視覚的に捉えることができるようになるかというと、
残念ながら私にはよくわからない。
実際、私は相関係数が 1 のときにそれが直線になる、
という説明を講義で行うときはベクトルの内積を使って説明している。
実は、相関係数が 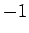 から 1 の間にあること、
そしてそれが
から 1 の間にあること、
そしてそれが 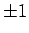 のときに点が直線的に並ぶこと、という部分は、
以下の シュワルツの不等式 から導かれる (ほぼ同等である)。
のときに点が直線的に並ぶこと、という部分は、
以下の シュワルツの不等式 から導かれる (ほぼ同等である)。
定理 1
(シュワルツの不等式)
正の実数 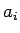 ,
, 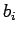 (
(
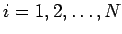 ) に対して、次の不等式が成り立つ。
) に対して、次の不等式が成り立つ。
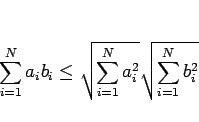 |
(2) |
なお、等号が成立するのは、
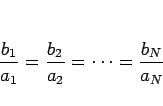 |
(3) |
の場合のみである。
このシュワルツの不等式は、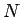 次元ベクトルの内積に対する不等式
次元ベクトルの内積に対する不等式
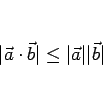
と同等であることが知られているし、
他にもシュワルツの不等式の証明は 2 次式の判別式を利用する方法、
あるいは (2) の両辺を 2 乗した式の差を 2 乗の和の形に変形する方法などがあるが、
いずれも途中の式変形がやや面倒であるし、
またその方はベクトルや内積は忘れておられるようだったので、
その方のアイデアを参考に、図形による証明を考えてみた。
それを 3 節で紹介する。
ただし、定理 1 全体を図形で考えるのは
さすがに無理があるので、それは前半の一部分だけである。
その前に、シュワルツの不等式と相関係数の関係について先に紹介しておく。
まず、シュワルツの不等式 (2) は、
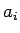 ,
, 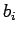 が正でなくても成立することに注意する。
それは、定理 1 が成り立つならば、
が正でなくても成立することに注意する。
それは、定理 1 が成り立つならば、
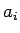 ,
, 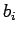 が正でなくても 0 であるものが含まれていなければ、
それらの絶対値を考えることで定理 1 より
が正でなくても 0 であるものが含まれていなければ、
それらの絶対値を考えることで定理 1 より
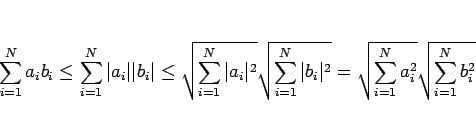
となるからである。この場合も等号が成立するのは、
この 2 つの不等号がともに等号となる場合だから、
すべての 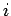 に対して
に対して 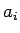 と
と 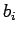 の符号が等しく (
の符号が等しく (
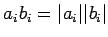 )、
かつ
)、
かつ
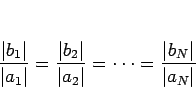
が成り立つ場合なので、よって結局 (3) と同じになる。
0 になるものが含まれている場合でも、
例えば簡単のため 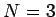 で、
で、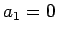 、
、
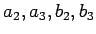 は 0 ではないとすると、
は 0 ではないとすると、
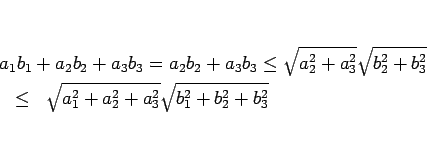
となってシュワルツの不等式 (2) は成立する。
等号が成り立つのは、上の 2 つの不等号が等号になる場合だから、
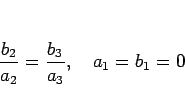
でなくてはならない。
今仮に 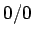 はすべての比に等しいとみることにすれば、
等号成立条件 (3) は、
0 が含まれていても成立することになる。
ただしその場合は、
はすべての比に等しいとみることにすれば、
等号成立条件 (3) は、
0 が含まれていても成立することになる。
ただしその場合は、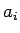 か
か 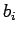 の一方が 0 ならば、
もう一方も 0 でなければならないことを意味する。
の一方が 0 ならば、
もう一方も 0 でなければならないことを意味する。
さて、相関係数に話を戻そう。
(2) の不等式のすべての 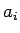 を
を 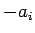 と変えた式を書けば、
と変えた式を書けば、
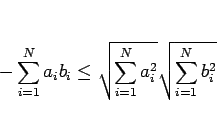
となるので、これと (2) を組み合わせれば、
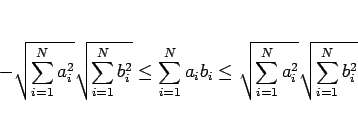 |
(4) |
となることがわかる。
(1) より、
この 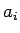 ,
, 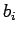 を
を
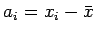 ,
,
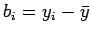 として、
辺々を平方根の式で割れば
として、
辺々を平方根の式で割れば
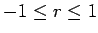 が言えることになる。
が言えることになる。
そして、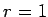 となるのは、条件 (3) と上の考察より、
すべての
となるのは、条件 (3) と上の考察より、
すべての 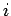 に対して
に対して 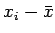 と
と 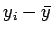 が同符号で
が同符号で
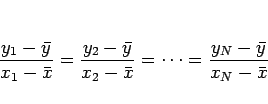
の場合となる。この比を 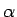 とすれば
とすれば 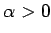 で、
すべての
で、
すべての 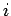 に対して
に対して
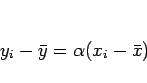
となるわけだから、すべての点 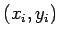 が傾き
が傾き 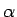 の直線
の直線
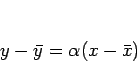
に乗ることとなる。
一方 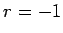 の場合は、
すべての
の場合は、
すべての 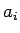 を
を 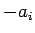 に置きかえた方の等号成立条件だから、
すべての
に置きかえた方の等号成立条件だから、
すべての 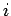 に対して
に対して 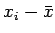 と
と 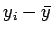 が異符号で
が異符号で
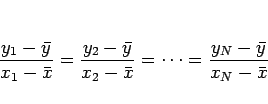
の場合となる。だからこの比を 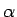 とすれば
とすれば 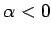 となる。
あとは、上と同様にすべての点が
となる。
あとは、上と同様にすべての点が
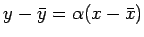 の上にあることになる。
の上にあることになる。
竹野茂治@新潟工科大学
2010年1月20日
![]() から 1 の間にあること、
そしてそれが
から 1 の間にあること、
そしてそれが ![]() のときに点が直線的に並ぶこと、という部分は、
以下の シュワルツの不等式 から導かれる (ほぼ同等である)。
のときに点が直線的に並ぶこと、という部分は、
以下の シュワルツの不等式 から導かれる (ほぼ同等である)。
![]() ,
, ![]() (
(
![]() ) に対して、次の不等式が成り立つ。
) に対して、次の不等式が成り立つ。
![]() 次元ベクトルの内積に対する不等式
次元ベクトルの内積に対する不等式
![]() ,
, ![]() が正でなくても成立することに注意する。
それは、定理 1 が成り立つならば、
が正でなくても成立することに注意する。
それは、定理 1 が成り立つならば、
![]() ,
, ![]() が正でなくても 0 であるものが含まれていなければ、
それらの絶対値を考えることで定理 1 より
が正でなくても 0 であるものが含まれていなければ、
それらの絶対値を考えることで定理 1 より
![]() で、
で、![]() 、
、
![]() は 0 ではないとすると、
は 0 ではないとすると、
![]() を
を ![]() と変えた式を書けば、
と変えた式を書けば、
![]() となるのは、条件 (3) と上の考察より、
すべての
となるのは、条件 (3) と上の考察より、
すべての ![]() に対して
に対して ![]() と
と ![]() が同符号で
が同符号で
![]() の場合は、
すべての
の場合は、
すべての ![]() を
を ![]() に置きかえた方の等号成立条件だから、
すべての
に置きかえた方の等号成立条件だから、
すべての ![]() に対して
に対して ![]() と
と ![]() が異符号で
が異符号で