6 S(k,r)
この節以降で、3 節で述べた方法での計算を行い、
それが 4 節での結果 (3) と一致することを確認する。
ただし、ここから先の話は元の問題からすれば本質的な話ではなく、
純粋に数学的な議論のみである。
また、この方針での計算はかなり大変であるので、
この後いくつかの節に分けて考察する。
3 節で考えたように、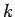 回余計にかって
回余計にかって 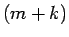 回で終わる確率は
回で終わる確率は
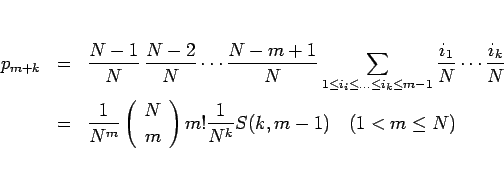
であるので、期待値 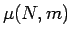 は、
は、
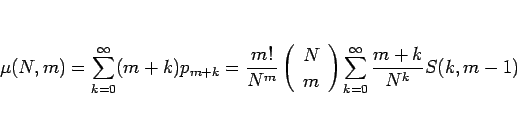 |
(4) |
となる。まずは、この 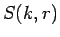 を
を 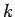 と
と 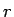 の式で表すところから始める。
なお、
の式で表すところから始める。
なお、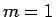 のときは明らかに
のときは明らかに 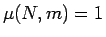 であるから、
以後
であるから、
以後 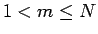 として考える。
として考える。
3 節で見たように、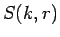 には、
には、
が成り立つ。
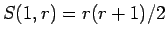 も言えていたが、これはむしろ (5) で
も言えていたが、これはむしろ (5) で
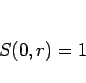 |
(7) |
であるとすれば得られるので、(7) が成り立つとすればよい。
なお、(5) を
この式の 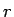 を
を 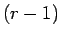 とした式と比較してみればわかるが、
とした式と比較してみればわかるが、
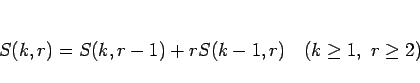 |
(8) |
が成り立つことに注意する。以後、この (6), (7), (8) から 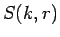 を求めていくことにするが、
逆にこれを満たす
を求めていくことにするが、
逆にこれを満たす 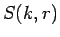 が一意に決定されることも容易にわかる。
が一意に決定されることも容易にわかる。
さて、今 (8) で 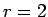 としてみると、
(6) より
としてみると、
(6) より
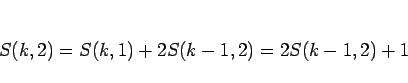
となるから、この両辺を 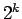 で割れば、
で割れば、
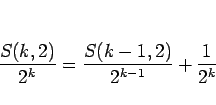
となるので、こ
の式にこの式の 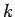 を
を 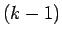 にしたものを代入する、
といったことを繰り返すことによって、
にしたものを代入する、
といったことを繰り返すことによって、
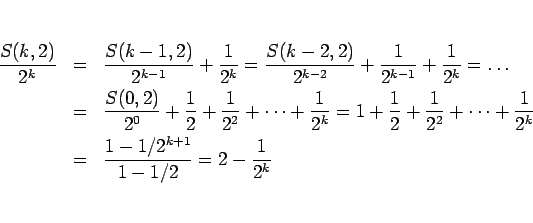
となり、よって
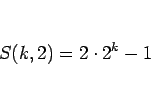 |
(9) |
が得られる。同様に、(8) で 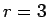 とすると
とすると
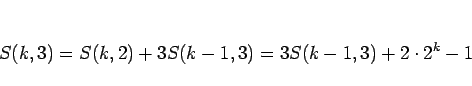
となるので、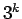 で割れば
で割れば
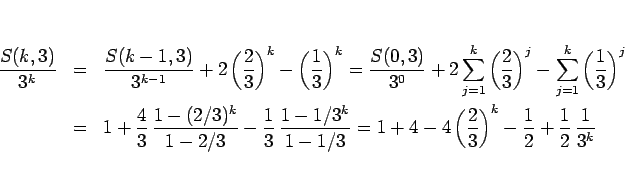
より、
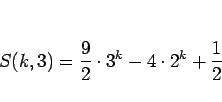 |
(10) |
のようになる。この、(9), (10) より、
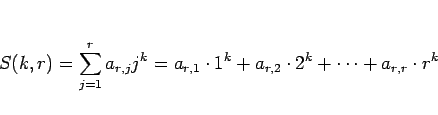 |
(11) |
の形であることが想像される。
もし、この (11) を (8) に代入して、
(6), (7), (8) を満たすように矛盾なく 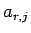 を決定できれば、
前に述べたようにそれを満たす
を決定できれば、
前に述べたようにそれを満たす 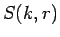 は一意であるから、
それで
は一意であるから、
それで 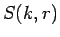 が得られることになる。
が得られることになる。
(11) を (8) に代入すると、
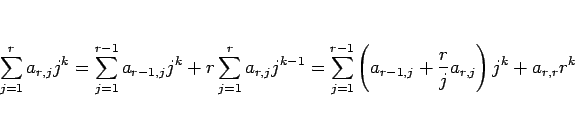
となる。よって、
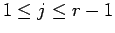 に対して、
に対して、
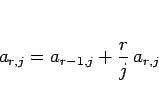
であればよく、これは、
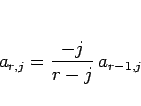
を意味するので、
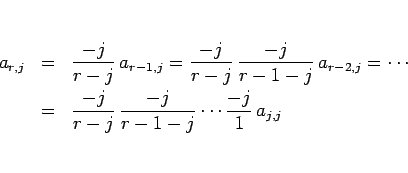
となり、
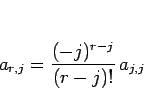 |
(12) |
となることになる。この 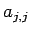 は次のように決定できる。
(11) に
は次のように決定できる。
(11) に  を代入すると (7) より
を代入すると (7) より
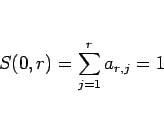
となるが、ここに (12) を代入して
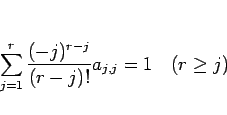 |
(13) |
が得られるが、
この (13) から次々 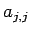 を求めることができる。
例えば、(13) に
を求めることができる。
例えば、(13) に 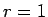 を代入すれば
を代入すれば
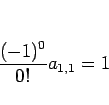
より 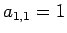 となり、
となり、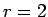 を代入すると、
を代入すると、
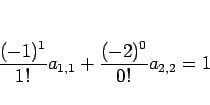
となるので、
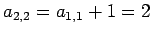 と求まる。以下、計算すると、
と求まる。以下、計算すると、
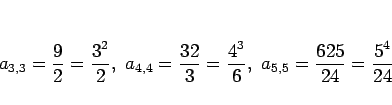
のようになるので、
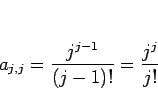 |
(14) |
となることが予想される。
これは実際に、(13) と帰納法を用いれば証明できる。
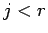 まで (14) が成り立つとすれば、
(13) により
まで (14) が成り立つとすれば、
(13) により 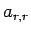 は、
は、
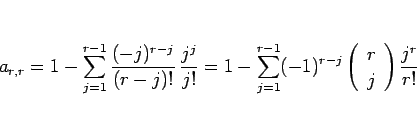
となる。ここで、
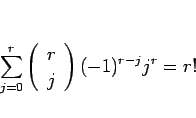 |
(15) |
であることを用いれば、
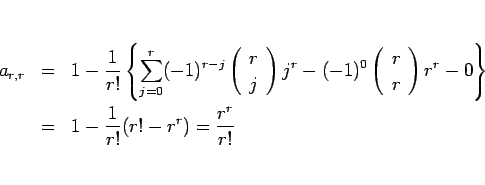
となるので、帰納法により (14) が成り立つことになる。
(15) は、母関数の方法を用いて以下のように証明できる。
二項定理により、
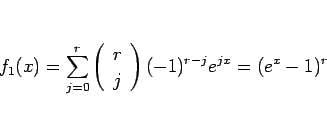
であるが、
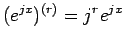 なので (15) は
なので (15) は 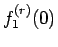 に等しいことになる。
に等しいことになる。
一方、テイラー展開を考えると、
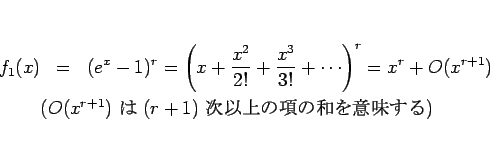
となるので
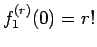 となり、
これで (15) が示されたことになる。
となり、
これで (15) が示されたことになる。
結局、(11), (12), (14) により、
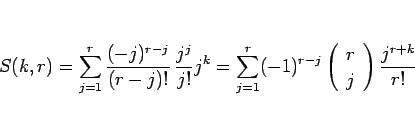 |
(16) |
となる。
これは、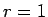 とすると
とすると
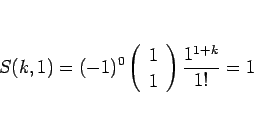
となり (6) も満たすので、
(6), (7), (8) を矛盾なく満たすことになり、
確かに (16) が成り立つことがわかる。
竹野茂治@新潟工科大学
2008年5月24日
![]() 回余計にかって
回余計にかって ![]() 回で終わる確率は
回で終わる確率は
![]() には、
には、
![]() を決定できれば、
前に述べたようにそれを満たす
を決定できれば、
前に述べたようにそれを満たす ![]() は一意であるから、
それで
は一意であるから、
それで ![]() が得られることになる。
が得られることになる。