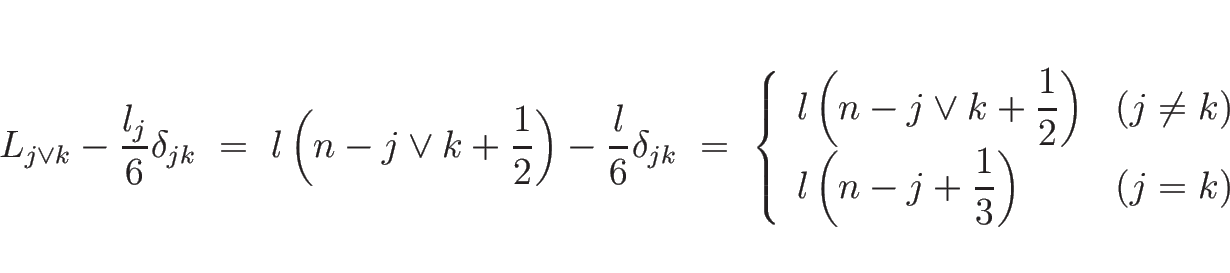5 相互力の消去
次に、ニュートンの運動方程式 (3) と
回転の方程式 (6) から
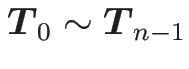 を消去する。
を消去する。
(3) より、
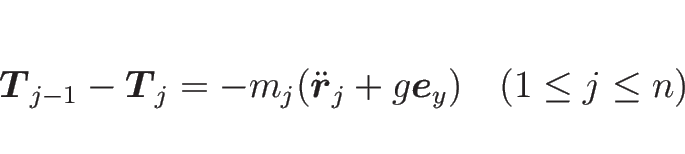 |
(7) |
となるが、これを 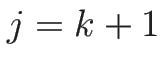 から
から 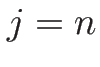 まで加えると、
まで加えると、
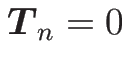 より
より
となるので、よって
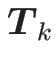 は
は
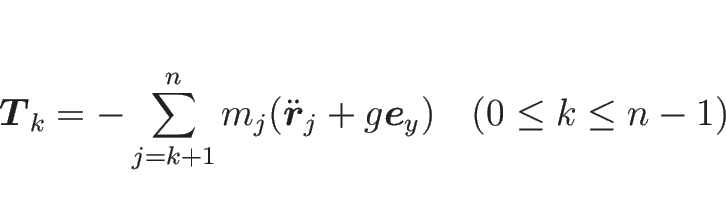 |
(8) |
と表される。そして、これにより
となり、これを (6) に代入すれば
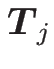 が
消去できることになる。
その前に式 (9) を
が
消去できることになる。
その前に式 (9) を
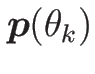 を用いて
表しておく。そのために、
を用いて
表しておく。そのために、
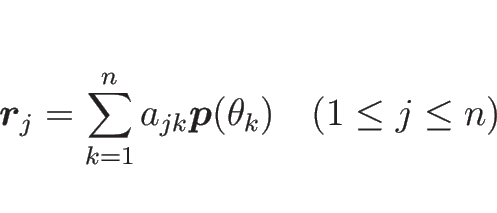 |
(10) |
と書くことにする。(2) より、この 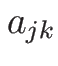 は
は
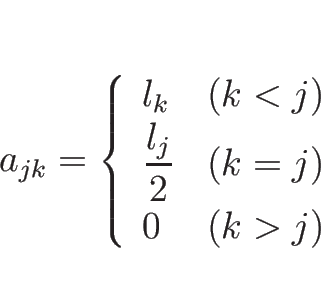 |
(11) |
となる。また、
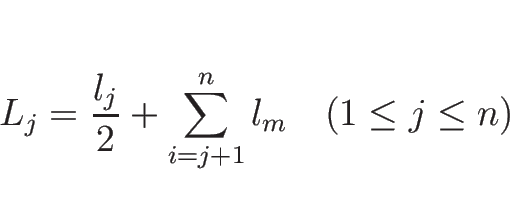 |
(12) |
とすれば、(9) の右辺 2 項目の係数は
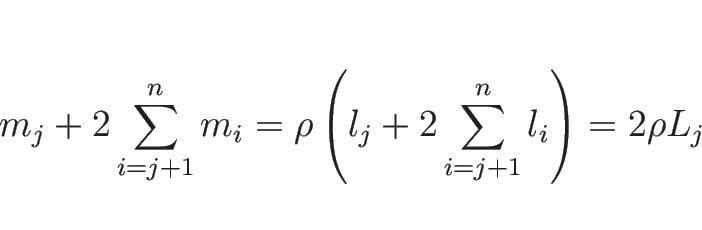 |
(13) |
と書ける。
(9) の右辺 1 項目の部分は、(10) により、
の形となるが、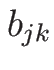 は
は
であり、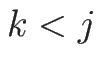 のときは (11) より
のときは (11) より
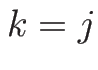 のときは、
のときは、
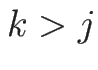 のときは、
のときは、
となり、よって、
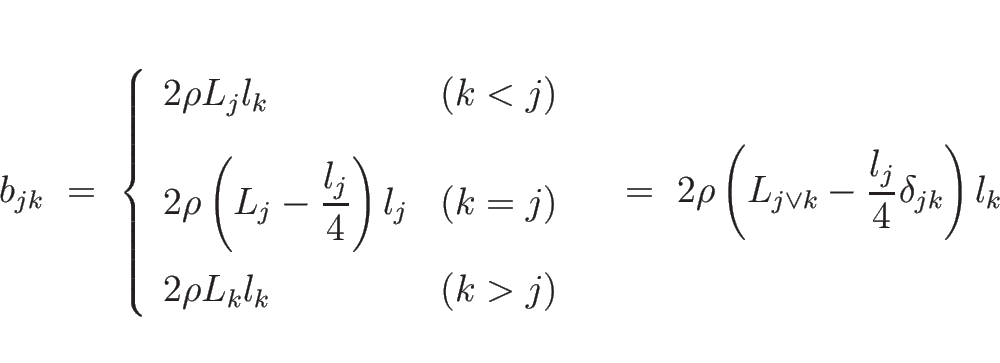 |
(15) |
となる。ここで、
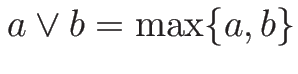 ,
, 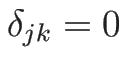 (
(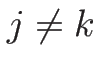 ),
), 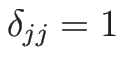 とする。
とする。
(15), および (13) により、
(9) は、
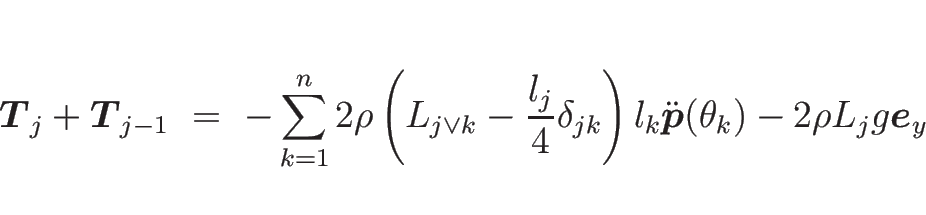 |
(16) |
となる。ここで、
であり、
なので、(16) より (6) は、
となり、これを 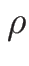 で割れば、
で割れば、
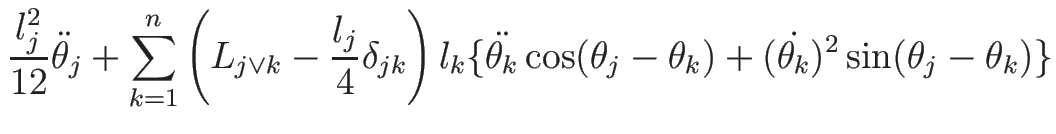 |
| |
|
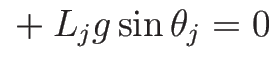 |
(17) |
となるが、この式の 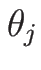 の微分の項をみると、
の微分の項をみると、
であり、また (17) の
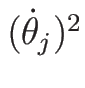 の
係数は 0 になるので、結局 (17) は
の
係数は 0 になるので、結局 (17) は
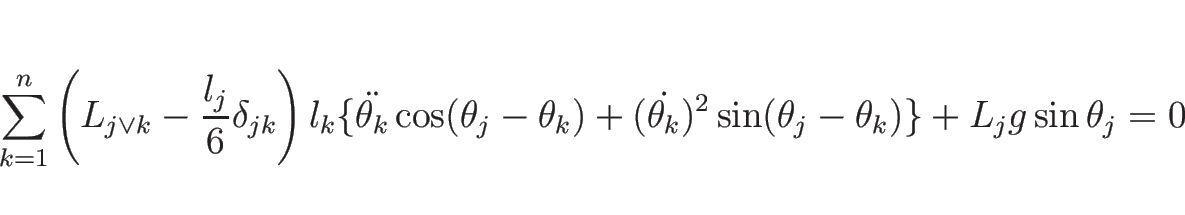 |
(18) |
と書くことができる。
これが、陽ではないが、
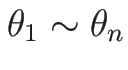 に対する 2 階の連立常微分方程式となる。
に対する 2 階の連立常微分方程式となる。
例えば、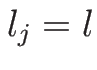 (
(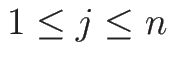 )、
すなわちすべての
)、
すなわちすべての 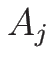 の長さが等しい場合は、
の長さが等しい場合は、
なので、この場合で 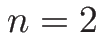 のときに方程式を書き下すと、
のときに方程式を書き下すと、
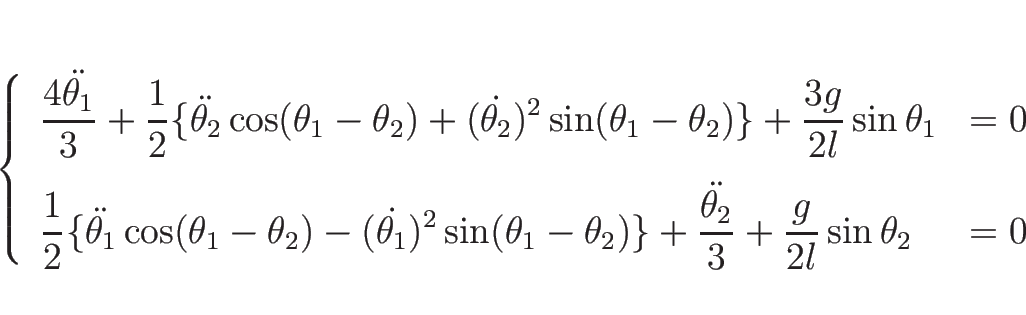 |
(19) |
となる。
最後に、(18) を行列の形で書いておく。
簡単のため、
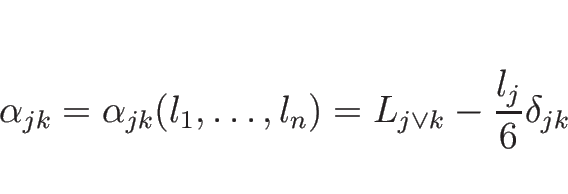 |
(20) |
と書くことにすると、
![\begin{displaymath}
A(\theta) = \left[\rule[-0.5zh]{0pt}{2zh}\
l_k\alpha_{jk}...
...t}{2zh}\
l_k\alpha_{jk}\sin(\theta_j-\theta_k) \right]_{j,k}\end{displaymath}](img100.png) |
(21) |
に対して、(18) は
![\begin{displaymath}
A(\theta)
\left[\begin{array}{c}\ddot{\theta_1} \vdots\\...
..._1\sin\theta_1 \vdots L_n\sin\theta_n\end{array}\right]
=0\end{displaymath}](img101.png) |
(22) |
の形となる。
なお、
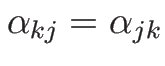 なので、
なので、
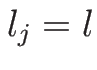 (
(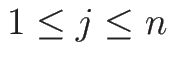 ) の場合は、
) の場合は、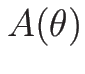 は対称行列、
は対称行列、
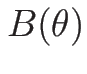 は交代行列となる。
は交代行列となる。
竹野茂治@新潟工科大学
2018-11-12
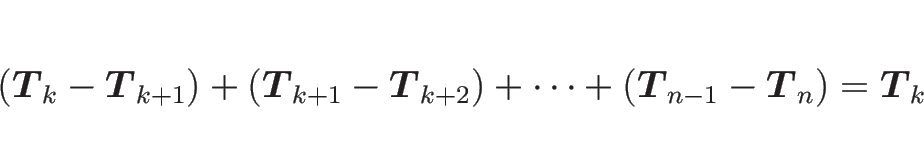
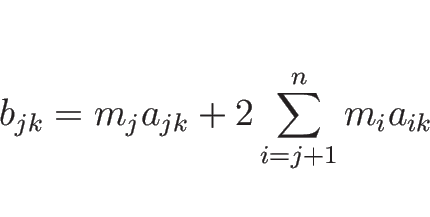
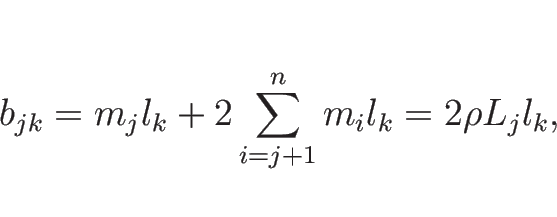
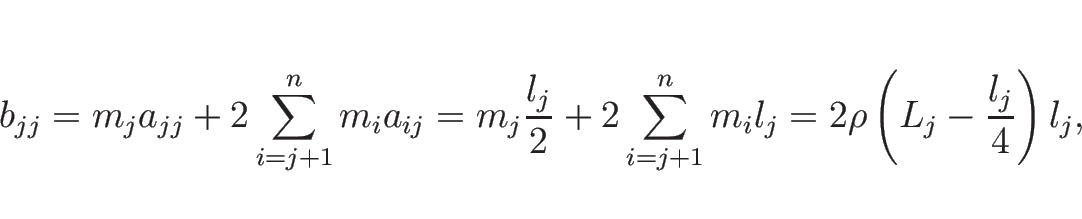
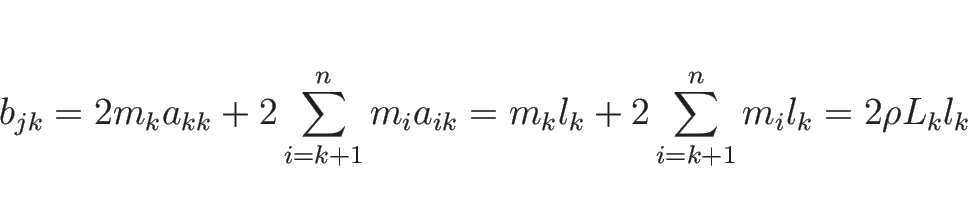
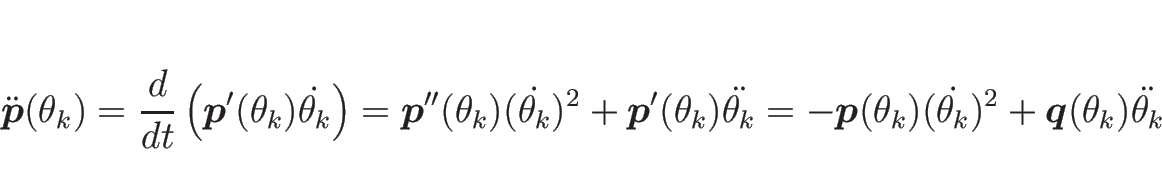
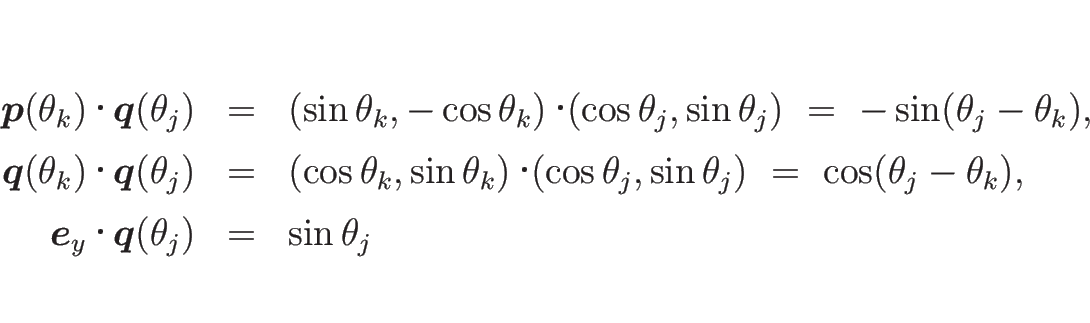
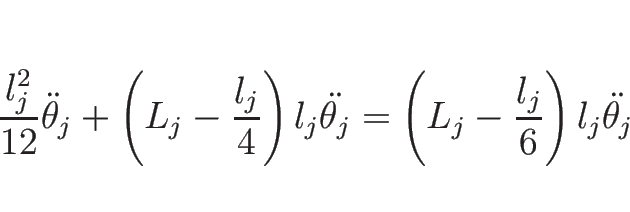
![]() (
(![]() )、
すなわちすべての
)、
すなわちすべての ![]() の長さが等しい場合は、
の長さが等しい場合は、