剛体の棒には、上から順に ![]() ,
, ![]() , ...,
, ..., ![]() と名前をつけ、
各
と名前をつけ、
各 ![]() の長さ、質量をそれぞれ
の長さ、質量をそれぞれ ![]() ,
, ![]() とするが、
剛体棒の線密度を
とするが、
剛体棒の線密度を ![]() とすれば
とすれば ![]() となる。
鉛直下向きの方向に対して、
となる。
鉛直下向きの方向に対して、![]() が右側に回転した角を
が右側に回転した角を ![]() とし、
とし、
![]() の中心 (= 重心) の位置ベクトルを
の中心 (= 重心) の位置ベクトルを
![]() ,
,
![]() と
と ![]() のつなぎ目の位置ベクトルを
のつなぎ目の位置ベクトルを
![]() と
する (図 2)。
と
する (図 2)。
鉛直下向きから右に ![]() 回転させた単位ベクトルを
回転させた単位ベクトルを
![]() 、
それをさらに
、
それをさらに ![]() 回転させたベクトルを
回転させたベクトルを
![]() とすると
とすると
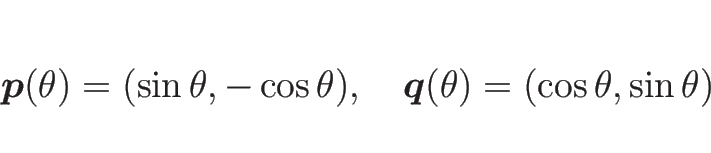
竹野茂治@新潟工科大学