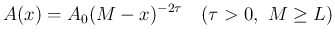
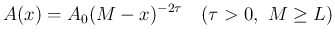
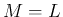 だと、開口端
だと、開口端 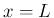 で
で 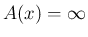 となるので現実的ではないし、
大きい
となるので現実的ではないし、
大きい 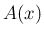 に対しては方程式そのものの妥当性も薄れてしまうが、
近似的な状況を考えるにはシンプルで、考えやすいモデルかもしれない。
しばらくは、
に対しては方程式そのものの妥当性も薄れてしまうが、
近似的な状況を考えるにはシンプルで、考えやすいモデルかもしれない。
しばらくは、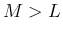 として考える。
として考える。
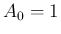 としてよい。
としてよい。
この場合は、
とし、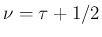 ,
, 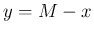 とすると、
とすると、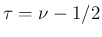 より、
より、
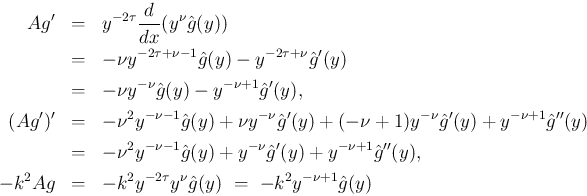
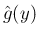 が満たす方程式は、
となる。これは、
が満たす方程式は、
となる。これは、
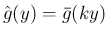 ,
, 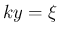 とすると、
とすると、
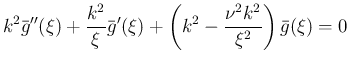
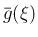 は、いわゆるベッセルの微分方程式
は、いわゆるベッセルの微分方程式
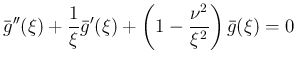
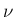 次ベッセル関数
次ベッセル関数 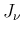 と
と 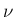 次ノイマン関数
次ノイマン関数 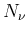 を用いて
を用いて
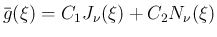
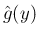 は、
となる。
は、
となる。
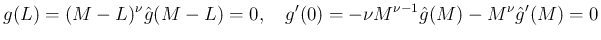
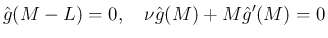
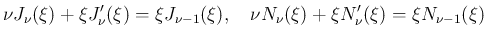
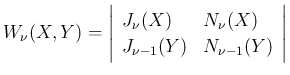
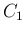 ,
, 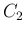 の条件式 (24), (27) の
係数行列の行列式は
の条件式 (24), (27) の
係数行列の行列式は
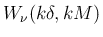 となるので、
この行列式が 0 でなければ
となるので、
この行列式が 0 でなければ 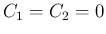 となって 0 以外の解が求まらないことになるので、
0 でない解が求まるためには
が必要となる。そしてこれを満たす
となって 0 以外の解が求まらないことになるので、
0 でない解が求まるためには
が必要となる。そしてこれを満たす 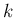 が存在すれば、その
が存在すれば、その 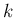 に対し
に対し
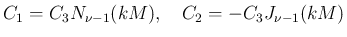
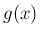 は
は
これまでのように、(28) を満たす 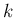 が
無数に存在するかどうか、
そしてそのとき周波数
が
無数に存在するかどうか、
そしてそのとき周波数 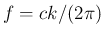 はどうなるかを考えたいが、
一般の
はどうなるかを考えたいが、
一般の 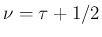 の場合には少し難しいので、
ここでは簡単のため、
の場合には少し難しいので、
ここでは簡単のため、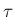 が整数
が整数 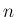 の場合を考えてみる。
ベッセル関数、ノイマン関数は
の場合を考えてみる。
ベッセル関数、ノイマン関数は 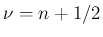 の場合は半ベッセル関数と呼ばれ、
の場合は半ベッセル関数と呼ばれ、
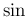 ,
, 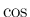 で表現されることが知られている ([1] 第 VI 篇 39)。
本節では主に
で表現されることが知られている ([1] 第 VI 篇 39)。
本節では主に 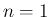 の場合を紹介するが、
これは断面の半径が
の場合を紹介するが、
これは断面の半径が
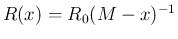 の円である場合に相当する。
の円である場合に相当する。
[1] (第 VI 篇 39) によれば、
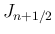 ,
, 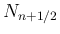 (
(
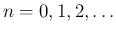 ) は、
) は、
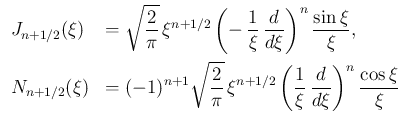
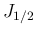 ,
, 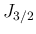 ,
, 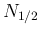 ,
, 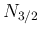 は、
となる。よって
は、
となる。よって 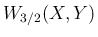 は、
は、
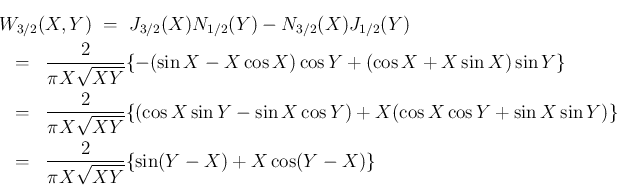
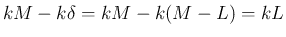 より、
より、
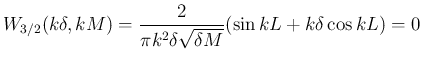
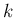 は、
となり、無数に存在することがわかる。
そして、(29) より解
は、
となり、無数に存在することがわかる。
そして、(29) より解 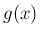 は、
は、
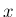 に依存する。
よって (32) の
に依存する。
よって (32) の 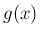 に対して「波長」という
呼び方はもはやこの解に対しては適切ではないが、
に対して「波長」という
呼び方はもはやこの解に対しては適切ではないが、
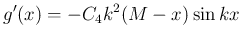
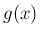 の極大極小の位置は、
の極大極小の位置は、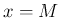 の前後で反転はするが、
の前後で反転はするが、
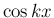 のその位置とほぼ同じになる。
つまり
のその位置とほぼ同じになる。
つまり 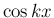 の波長と同じ「波長」らしきものが
の波長と同じ「波長」らしきものが 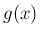 にも
存在すると見ることができ、その「波長」は
(31) の
にも
存在すると見ることができ、その「波長」は
(31) の 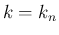 に対して
に対して
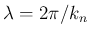
周波数の方は、(31) の 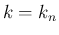 に対して
に対して
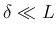 であれば
であれば
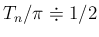 となるので、
となるので、
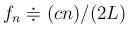 となるから、
その自然倍音列は直開管の自然倍音列の周波数に近くなる。
となるから、
その自然倍音列は直開管の自然倍音列の周波数に近くなる。
最後に 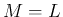 の場合の話も少し書いておく。
この場合も、(21) の変換によって
ベッセルの方程式 (22) が得られ、
その一般解が (23) と表される
ことまでは同じである。
の場合の話も少し書いておく。
この場合も、(21) の変換によって
ベッセルの方程式 (22) が得られ、
その一般解が (23) と表される
ことまでは同じである。
境界条件の 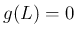 の方は、
この場合は
の方は、
この場合は
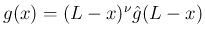 より
より 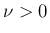 なら
自然に
なら
自然に 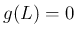 となりそうであるが、実はそんなに簡単でもない。
となりそうであるが、実はそんなに簡単でもない。
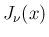 は
は
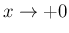 で
で
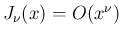 な
ので
な
ので 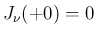 であるが、
であるが、
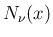 の方は
の方は
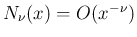 なので
なので
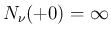 となる。
となる。
ただ、
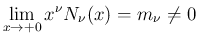
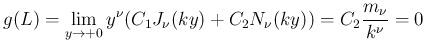
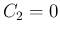 となり、よってこの場合
となり、よってこの場合
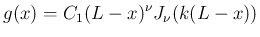
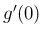 は (26) より、
は (26) より、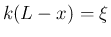 とすれば、
とすれば、
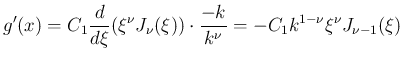
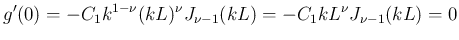
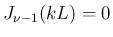
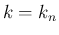 が満たすべき条件となる。
が満たすべき条件となる。
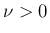 ならば
ならば
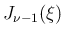 には、
には、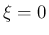 以外に
無限個の離散的な零点
以外に
無限個の離散的な零点
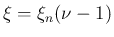 (
(
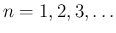 ) が
存在することが知られていて、正確な値を知ることは容易ではないが、
漸近公式なども知られている ([1] 第 VI 篇 36)。
) が
存在することが知られていて、正確な値を知ることは容易ではないが、
漸近公式なども知られている ([1] 第 VI 篇 36)。
特に、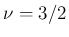 (
(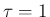 ) の場合は、(30) より、
) の場合は、(30) より、
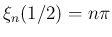 なので、
なので、
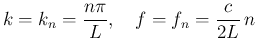
 (
( ) とした
ものにも一致している。
) とした
ものにも一致している。
また、この場合の解 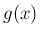 は、
は、
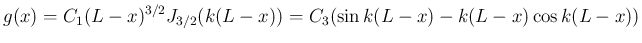
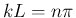 より、
より、
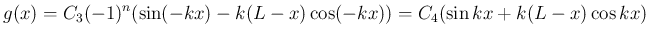
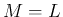 としたものに一致する。
としたものに一致する。
つまり、あまり現実的ではなさそうな 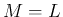 の式は、
の式は、
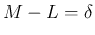 が小さい場合の話を、
ある程度ちゃんと近似していることがわかる。
が小さい場合の話を、
ある程度ちゃんと近似していることがわかる。
竹野茂治@新潟工科大学