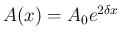
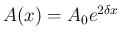 (
(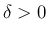 ) の場合を考える。
これは、断面の半径が
) の場合を考える。
これは、断面の半径が
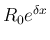 の指数関数である円である
管に対応する。これも
の指数関数である円である
管に対応する。これも 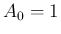 としてよい。
としてよい。
この場合は、
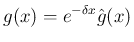
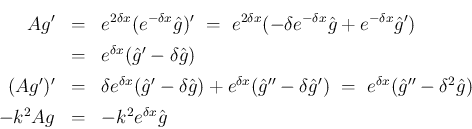
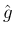 は
を満たす。
は
を満たす。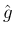 の境界条件は、
の境界条件は、
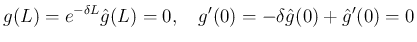
(18) の一般解は、
 と
と  の大小により解の形が分かれる。
の大小により解の形が分かれる。
まず、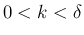 の場合は
の場合は
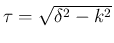 に対して、
に対して、
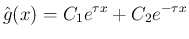
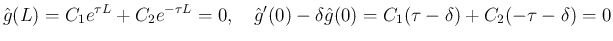
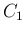 ,
, 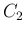 の係数行列の行列式は、
の係数行列の行列式は、
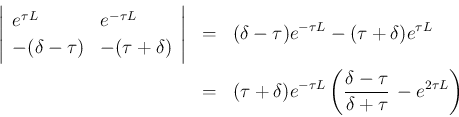
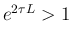 ,
,
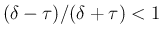 なので、
この行列式は負となり、よって
なので、
この行列式は負となり、よって 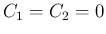 となるので不可。
となるので不可。
次に、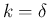 の場合は
の場合は
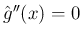 より
より
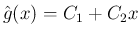 と
なり、(19) より、
と
なり、(19) より、
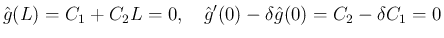
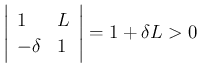
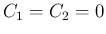 となって不可。
となって不可。
よって 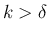 の場合のみ 0 でない解が存在する可能性がある。
この場合
の場合のみ 0 でない解が存在する可能性がある。
この場合
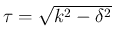 とすると、
(18) より
とすると、
(18) より
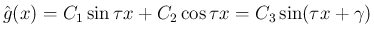
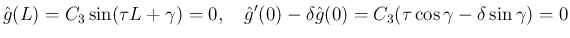
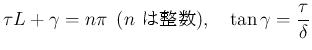
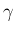 を消去すると、
を消去すると、
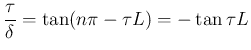
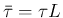 (
(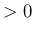 ) とすると
) とすると
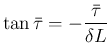
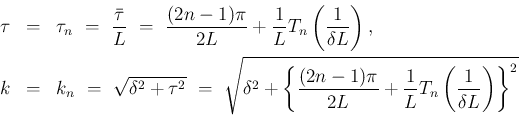
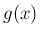 は、
は、
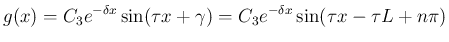
 と周波数
と周波数 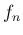 は、
は、
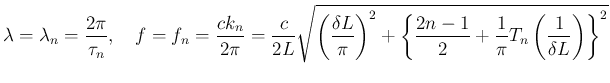
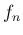 の挙動を決めるのは
の挙動を決めるのは 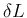 で、
で、
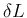 が大きい、すなわち管の曲がりが急な場合は
が大きい、すなわち管の曲がりが急な場合は
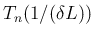 は
は 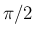 に近くなるが、
この場合
に近くなるが、
この場合 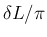 の項が無視できなくなるので、
自然倍音列は直開管に近いとも直閉管に近いともいいにくい状況になる。
逆に
の項が無視できなくなるので、
自然倍音列は直開管に近いとも直閉管に近いともいいにくい状況になる。
逆に 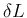 が小さい、すなわち管の曲がりがゆるやかな場合は
が小さい、すなわち管の曲がりがゆるやかな場合は
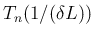 は 0 に近く、
よって
は 0 に近く、
よって 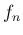 は直閉管に近い状況になる。
は直閉管に近い状況になる。
つまり、この指数関数形では、 自然倍音列を直開管に近づけるのは難しいかもしれない。
竹野茂治@新潟工科大学