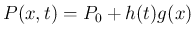 (4)
(4)
定在波は、通常は時間的に周期的な解で、 左右に移動せず振幅のみ変化する解を指すが、 それは、変数分離形の解
で (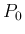 は大気圧)、
は大気圧)、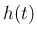 が周期的なものとして表現される。
必ずしもこのような解が存在することは明かではないが、
線形の波動方程式では良くこの形の解が利用され、
さらにその形の解の重ね合わせで、
より一般的な解を構成すること (フーリエ級数解など) も良く行われている。
が周期的なものとして表現される。
必ずしもこのような解が存在することは明かではないが、
線形の波動方程式では良くこの形の解が利用され、
さらにその形の解の重ね合わせで、
より一般的な解を構成すること (フーリエ級数解など) も良く行われている。
方程式 (3) の境界条件は、
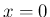 が息の入る口で、
が息の入る口で、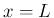 が息や音の出口とすると、出口では、
が息や音の出口とすると、出口では、
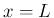 が圧力の節であることも意味する。
つまり管楽器のほぼ出口付近では音は最小であることになる。
が圧力の節であることも意味する。
つまり管楽器のほぼ出口付近では音は最小であることになる。
一方もう一つの境界である入口 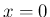 では、
マウスピースによる圧力振動を入力するという条件
では、
マウスピースによる圧力振動を入力するという条件
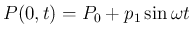
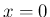 が圧力の腹であること、
すなわち
を課すことにする。
これは、振動を与える入力口が最も振動の激しいところ、ということを
意味するが、一応閉管の反射壁の条件とも対応する。しかし、
こう考えることが現象と比較して適切なのかどうかはよくわからない。
が圧力の腹であること、
すなわち
を課すことにする。
これは、振動を与える入力口が最も振動の激しいところ、ということを
意味するが、一応閉管の反射壁の条件とも対応する。しかし、
こう考えることが現象と比較して適切なのかどうかはよくわからない。
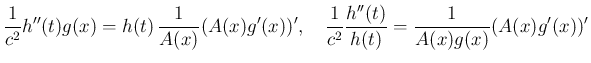
 のみの式、右辺は
のみの式、右辺は  のみの式となるので、
結果としてこの式は定数となり、よって
の 2 本の常微分方程式に分離できる。
境界条件 (5), (6) は、
のみの式となるので、
結果としてこの式は定数となり、よって
の 2 本の常微分方程式に分離できる。
境界条件 (5), (6) は、
 ,
,  で書くと、
で書くと、
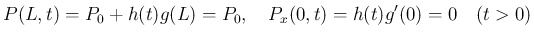
 の場合は、(7) の
の場合は、(7) の 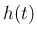 は指数関数で表されるか (
は指数関数で表されるか (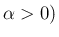 、
または 1 次式 となり (
、
または 1 次式 となり (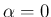 )、周期関数にはならないし、
その場合の
)、周期関数にはならないし、
その場合の 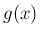 の解も
境界条件 (5), (6) を満たすものは
自明なもの
の解も
境界条件 (5), (6) を満たすものは
自明なもの 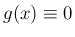 以外にはない。
以外にはない。
それを示す簡単な例として、直管の場合
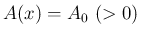 の場合を考えてみる。
の場合を考えてみる。
この場合は、(7) は
となる。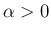 ならば、この解は良く知られているように、
ならば、この解は良く知られているように、
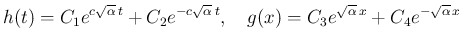
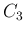 ,
, 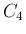 の連立方程式の係数行列の行列式は、
の連立方程式の係数行列の行列式は、
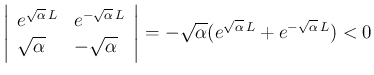
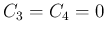 しかない。
よって
しかない。
よって 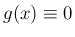 となり、解は必然的に自明な定数解
となり、解は必然的に自明な定数解 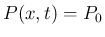 に
なってしまう。
に
なってしまう。
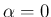 の場合は、(9) の解は、
の場合は、(9) の解は、
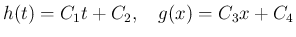
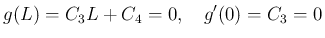
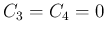 となってしまう。
となってしまう。
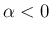 の場合は、
の場合は、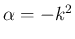 (
(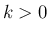 ) とすると、
) とすると、
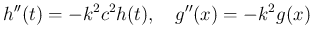
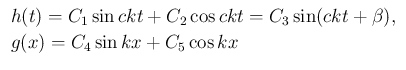
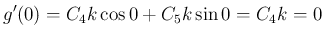
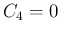 、よって
、よって
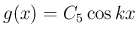 、
、
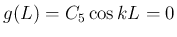
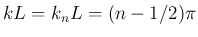 (
(
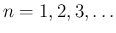 ) となり、
) となり、
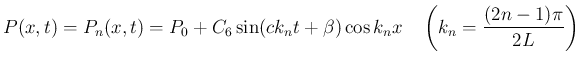
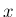 方向の周期
方向の周期
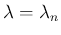 と、
周波数、すなわち
と、
周波数、すなわち 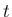 方向の周期の逆数
方向の周期の逆数 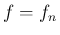 は、
は、
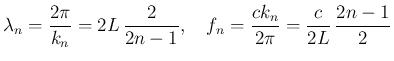
本稿では定在波を考察するため、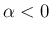 の場合を考えることとし、
以後
の場合を考えることとし、
以後 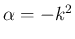 (
(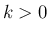 ) とする。
) とする。
竹野茂治@新潟工科大学