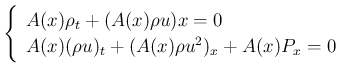 (1)
(1)
楽器のように断面が一様でない管中の気体の 1 次元的な方程式 (連立偏微分方程式) は以下の通り ([9])。
ここで、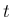 は時刻、
は時刻、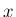 は
は 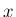 軸に沿った座標、
軸に沿った座標、
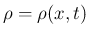 (未知関数) は気体密度、
(未知関数) は気体密度、
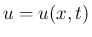 (未知関数) は気体速度、
(未知関数) は気体速度、
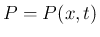 (未知関数) は単位面積当たりの気体圧力、
(未知関数) は単位面積当たりの気体圧力、
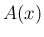 (既知関数) は
(既知関数) は 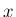 軸に垂直な面での
軸に垂直な面での 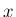 での断面積とする。
ただし、気体の粘性は無視しているし、
での断面積とする。
ただし、気体の粘性は無視しているし、
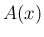 が大きくなりすぎると気体を 1 次元的な運動と見ることが
できなくなるので、方程式の解と実際の現象とのずれが大きくなるだろう。
が大きくなりすぎると気体を 1 次元的な運動と見ることが
できなくなるので、方程式の解と実際の現象とのずれが大きくなるだろう。
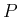 は
は 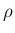 のみの関数と考え、
のみの関数と考え、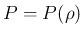 とすると、
音速
とすると、
音速 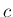 は、
は、
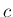 は一定であると考え、
また楽器管内の流速は
は一定であると考え、
また楽器管内の流速は 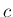 に比べだいぶ小さいと考え (多分音速の数パーセント程度)、(1) の
に比べだいぶ小さいと考え (多分音速の数パーセント程度)、(1) の 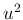 の項は無視する。
こうすると (1) より、
の項は無視する。
こうすると (1) より、
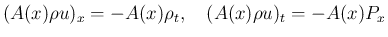
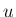 を消去すれば
を消去すれば
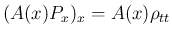
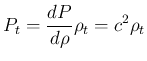
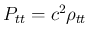 となり、
よって、圧力
となり、
よって、圧力 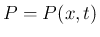 のみを未知関数とする方程式
が得られる。
これがウェブスターのホーン方程式である。
本稿ではこの方程式を使って考察を行う。
のみを未知関数とする方程式
が得られる。
これがウェブスターのホーン方程式である。
本稿ではこの方程式を使って考察を行う。
なお、ホーン方程式 (3) は圧力 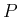 を未知関数としているが、
高校の物理では、縦波は圧力ではなく「変位」を未知関数として
説明することが多い。
変位と圧力では、定在波の「腹」と「節」の関係が逆になるので
注意が必要である。
を未知関数としているが、
高校の物理では、縦波は圧力ではなく「変位」を未知関数として
説明することが多い。
変位と圧力では、定在波の「腹」と「節」の関係が逆になるので
注意が必要である。
竹野茂治@新潟工科大学