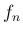
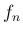 や波長
や波長 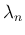 には、以下の関係があることが紹介される。
には、以下の関係があることが紹介される。
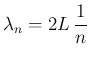 ,
周波数
,
周波数
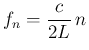 (
(
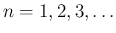 )
)
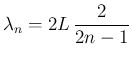 ,
周波数
,
周波数
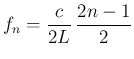 (
(
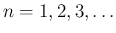 )
)
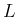 は管長、
は管長、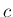 は音速である。
は音速である。
これらの周波数の音は、
管に穴やバルブがなくても自然に「鳴りやすい」音なので、
「自然倍音」とも呼ばれる。
開管の場合には 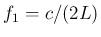 の整数倍が自然倍音列で、
閉管の場合には
の整数倍が自然倍音列で、
閉管の場合には 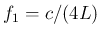 の奇数倍が自然倍音列となり、
少しずれがあることがわかる。
の奇数倍が自然倍音列となり、
少しずれがあることがわかる。
一方、息を吹き込んで音を出す管楽器も、穴やバルブを使わなくても とびとびの自然倍音列が出るのであるが、 その周波数は、管としての共鳴音の自然倍音列と同じとは限らない。 それは、息という流体を吹き込んでいるためによる影響、 音を発生させる仕組みや形状などの影響による。 ただ、楽器としての自然倍音列が、 共鳴管としての自然倍音列に追従する形で現れるのは間違いないだろうと思うので、 本稿ではホーン方程式に従って計算される、 共鳴管としての自然倍音列について考察する。
ちゃんとした楽器としての自然倍音列に関しては、 音響学の専門書、例えば [4],[5] 等や、 あるいは音響学会等の論文などを見るべきだろうと思う。
特に本稿で考えたいのは、 管楽器の断面形状と自然倍音列の関係についてである。 フルート以外の多くの管楽器は、管の形状としては閉管 (息を入れる方の口が壁になる) であり、 よって直管であれば本来は最低音の奇数倍の自然倍音列が出るはずであるが、 金管楽器もまたは木管楽器のオーボエも、自然倍音列は、 むしろ直管の開管のような最低音の整数倍の自然倍音列が出ることが 知られている。
これは、管の形状、特に出口部分が極端に広がっているため、 という説明がなされるが (例えば [6])、 それをホーン方程式で説明ができるのかどうかを考察したいと思う。
竹野茂治@新潟工科大学