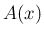
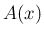 に対して、
に対して、
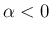 の場合の方程式 (7)、
すなわち、
の場合の方程式 (7)、
すなわち、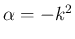 (
(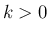 ) での
) での 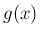 に対する
2 階常微分方程式の境界値問題
と、
に対する
2 階常微分方程式の境界値問題
と、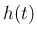 の解
の解
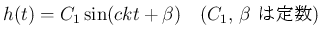
まず本節では
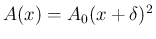
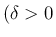 ) とする。
これは、管が円錐の一部の場合に相当する。
なお、(11) の両辺で
) とする。
これは、管が円錐の一部の場合に相当する。
なお、(11) の両辺で 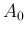 は消えてしまうので、
最初から
は消えてしまうので、
最初から 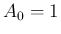 として構わないことに注意する。
として構わないことに注意する。
ちなみに、管楽器のうち、オーボエは円錐管であるらしい。
今、
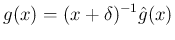
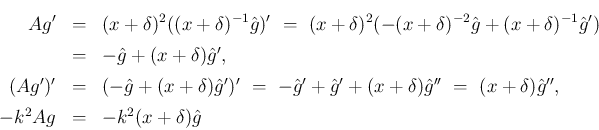
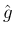 に関する方程式は
に関する方程式は
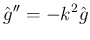
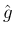 の条件に書き直すと、
の条件に書き直すと、
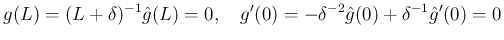
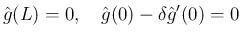
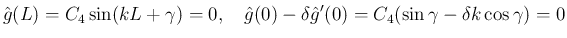
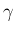 を消去すると、
となる。この (14) を満たす
を消去すると、
となる。この (14) を満たす 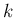 により
により 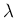 ,
, 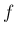 が決定する。
が決定する。
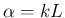 とすると、(14) は、
とすると、(14) は、
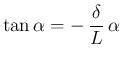
この形の超越方程式は今後も出てくるので、
の の解について、ここに少しまとめておく。
の解について、ここに少しまとめておく。
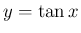 のグラフと直線
のグラフと直線 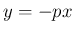 の交点の
の交点の 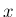 座標が (15) の解となるので、その解は無限に存在し、
の形になる。ここで
座標が (15) の解となるので、その解は無限に存在し、
の形になる。ここで 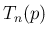 は以下の性質を満たす。
は以下の性質を満たす。
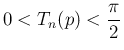
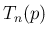 は
は 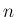 に関して単調減少で
に関して単調減少で
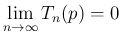
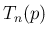 は
は 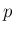 に関して単調減少で
に関して単調減少で
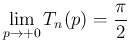 ,
,
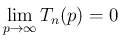
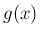 は、
(13) より
は、
(13) より
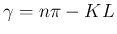 なので、
なので、
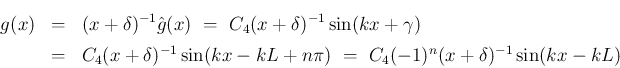
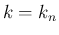 に対して
に対して
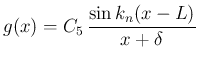
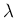 と周波数
と周波数 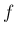 は、
は、
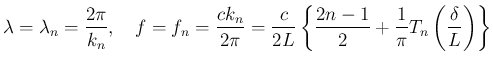
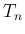 の性質により、
の性質により、
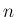 がかなり大きければ
がかなり大きければ 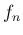 は
は 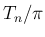 は 0 に近くなるが、
は 0 に近くなるが、
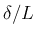 がかなり小さければ
がかなり小さければ 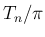 は
は 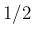 に近い。
よって
に近い。
よって 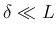 であれば、
円錐管の自然倍音列の最初の方は、
直閉管の自然倍音列よりも直開管の自然倍音列に近くなることになる。
であれば、
円錐管の自然倍音列の最初の方は、
直閉管の自然倍音列よりも直開管の自然倍音列に近くなることになる。
竹野茂治@新潟工科大学