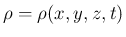 ,
, 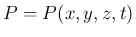 , および 3 次元速度ベクトル
, および 3 次元速度ベクトル
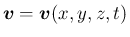 に対する
圧縮性オイラー方程式
に対する
圧縮性オイラー方程式
一方、空間 3 次元の未知関数
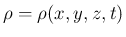 ,
, 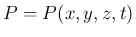 , および 3 次元速度ベクトル
, および 3 次元速度ベクトル
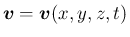 に対する
圧縮性オイラー方程式
に対する
圧縮性オイラー方程式
そのためには、3 次元方程式 (6) を 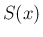 で
で 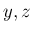 に関して積分すればよさそうであるが、
実は少し面倒なところがあるので、本節ではその前段階として、
3 次元方程式 (6) を
に関して積分すればよさそうであるが、
実は少し面倒なところがあるので、本節ではその前段階として、
3 次元方程式 (6) を 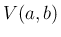 で積分することで
改めて積分方程式を導き、そこから (1) に対応する
方程式を導いてみる。
で積分することで
改めて積分方程式を導き、そこから (1) に対応する
方程式を導いてみる。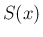 での積分による直接の導出については、
4 節で考察する。
での積分による直接の導出については、
4 節で考察する。
まず、議論を少し簡単にするため、密度 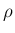 と圧力
と圧力 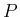 は
は 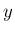 ,
, 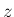 によらない
によらない 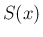 内で一様な関数であるとする。
内で一様な関数であるとする。
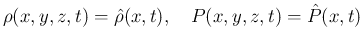
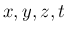 の関数
の関数 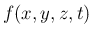 の、
の、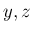 に関する
断面平均を
に関する
断面平均を 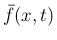 と書くことにする。
と書くことにする。
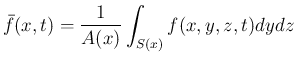
壁  では、
では、
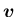 は境界条件
は境界条件
(6) の 1 本目を、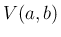 で積分する。
で積分する。
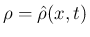 は
は 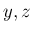 に依らないので、
に依らないので、
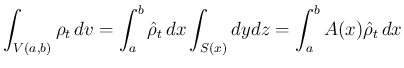
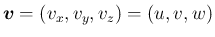 とすると、発散定理より、
とすると、発散定理より、
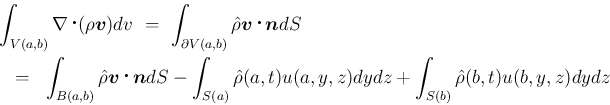
 上の
面積分は 0 となるので、
結局 (6) の 1 本目の積分は、
上の
面積分は 0 となるので、
結局 (6) の 1 本目の積分は、
![$\displaystyle \int_a^bA(x)\hat{\rho}_t\,dx
+ \left[\hat{\rho}\int_{S(x)}udydz\right]_a^b = 0
$](img68.png)
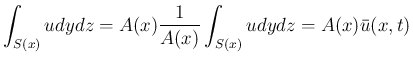
![$\displaystyle \int_a^bA(x)\hat{\rho}_t\,dx
+ \left[\hat{\rho}A(x)\bar{u}\right]_a^b
= \int_a^b\{A(x)\hat{\rho}_t +(\hat{\rho}A(x)\bar{u})_x\}dx = 0
$](img70.png)
 の任意性により
が得られる。これは、
の任意性により
が得られる。これは、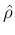 ,
, 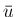 に関する (1) の 1 本目の式に対応する。
に関する (1) の 1 本目の式に対応する。
次は運動量。まずは、(6) の 2 本目の、
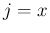 に対する式を積分する。
に対する式を積分する。
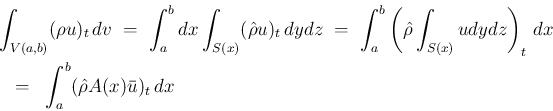
![\begin{eqnarray*}\lefteqn{\int_{V(a,b)}\nabla\mathop{・}(\rho u\mbox{\boldmath {$...
...ho}A(x)\overline{u^2}(x,t)\right]_a^b
+\int_a^bA(x)\hat{P}_x\,dx\end{eqnarray*}](img77.png)
![$\displaystyle \int_a^bA(x)(\hat{\rho}\bar{u})_t\,dx
+\left[\hat{\rho}A(x)\overline{u^2}(x,t)\right]_a^b
+\int_a^bA(x)\hat{P}_x\,dx = 0
$](img78.png)
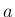 ,
, 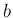 の任意性により、
が得られる。これは、(1) の 2 本目と
完全に同じものではないが、
の任意性により、
が得られる。これは、(1) の 2 本目と
完全に同じものではないが、
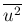 が近似的に
が近似的に 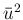 に等しいと考えれば (例えば
に等しいと考えれば (例えば 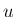 が
が 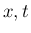 にのみ依存する場合など)、
にのみ依存する場合など)、
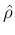 ,
, 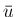 に関する (1) の 2 本目の式に対応する。
に関する (1) の 2 本目の式に対応する。
同様に、(6) の 2 本目の、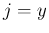 に対する式を
積分してみると、
に対する式を
積分してみると、
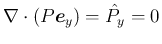
![\begin{eqnarray*}\int_{V(a,b)}(\rho v)_t\,dv
&=&
\int_a^b (\hat{\rho}A(x)\bar{...
...\right]_a^b
\\ &=&
\left[\hat{\rho}A(x)\overline{uv}\right]_a^b\end{eqnarray*}](img84.png)
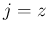 の式を積分すれば、
が得られる。
の式を積分すれば、
が得られる。
最後はエネルギー。(6) の 3 本目を積分する。
![\begin{eqnarray*}\lefteqn{\int_{V(a,b)}(\rho E)_t\,dv
\ =\
\int_a^b \left(\ha...
...
\left[A(x)(\hat{\rho}\,\overline{Eu}+\hat{P}\bar{u})\right]_a^b\end{eqnarray*}](img88.png)
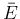 ,
, 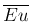 は、
は、
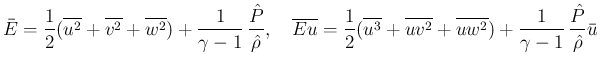
竹野茂治@新潟工科大学